Способ тестирования оперативных запоминающих устройств

Способ тестирования оперативных запоминающих устройств

Иллюстрации

Показать все

Реферат

Изобретение относится к цифровой вычислительной технике и предназначено для решения задачи функционального тестирования статических оперативных запоминающих устройств (ОЗУ) как на стадии их производства, так и на стадии их эксплуатации, например, в микропроцессорных системах.

Наиболее близким по технической сути является способ тестирования ОЗУ, представленный в [1].

Данный способ тестирования ОЗУ заключается в том, что путем использования P-разрядного генератора псевдослучайных чисел на основе циклического регистра сдвига с линейной обратной связью и периодом повторения М, структуру которого предварительно определяют на основе системы неравенств

P≥L, M=(2^P-1)≥N, К≥L,

где L - разрядность тестируемого ОЗУ;

N - количество ячеек тестируемого ОЗУ,

проводят подряд не менее К циклов тестирования, в каждом из которых выполняют, последовательно чередуя, процедуру записи тестовых L-разрядных псевдослучайных чисел во все N ячейки ОЗУ, а затем процедуру чтения из каждой ячейки ОЗУ записанных в них данных и сравнения их с тестовыми псевдослучайными числами, причем для формирования тестовых псевдослучайных чисел сначала в генератор псевдослучайных чисел записывают новое начальное двоичное P-разрядное число, отличное от нуля, L-разрядов которого позже используют как первое тестовое число, затем последовательно осуществляют (N-1) циклических сдвигов в регистре сдвига с линейной обратной связью, и таким образом формируют все N L-разрядные тестовые числа.

При данном способе тестирования ОЗУ время тестирования не зависит от разрядности ОЗУ, а также полагается, что вероятность необнаружения ошибки в ОЗУ оценивается величиной Р_н=2^-К, (К - количество циклов тестирования ОЗУ), если (2^P-1)≥N.

Заявленная вероятность необнаружения ошибки данного способа тестирования ОЗУ является некорректной по следующим причинам: не конкретизирован тип ошибки; при увеличении количества циклов тестирования больше величины К≥2^P-1 (т.е. больше цикла повторения двоичной псевдослучайной последовательности) может быть оценена лишь устойчивость тестируемого ОЗУ к случайным сбоям, а эффективность обнаружения константных неисправностей в элементах памяти и неисправностей, обусловленных взаимовлиянием данных между элементами памяти, не улучшается по сравнению с той, которая достигается за К=2^P-1 циклов тестирования. Известно [2], что необходимое и достаточное условие функционального тестирования ОЗУ может быть достигнуто только в том случае, когда достигается индивидуальная различимость каждого элемента памяти. Под различимостью понимается то, что в каждый отдельный элемент памяти будет записываться отличный от всех других элементов памяти К-разрядный последовательный код, формируемый в них за К циклов тестирования. Обеспечение такой различимости элементов памяти гарантирует обнаружение всех константных неисправностей и максимизирует обнаружение неисправностей, обусловленных информационным взаимовлиянием элементов памяти, так как для произвольно выбранной пары элементов памяти будет обеспечен их «бинарный антагонизм» - одновременно в один из элементов будет записываться 1, а в другой - 0. Применительно к данному способу, различимость элементов памяти должна обеспечиваться за счет того, что проводится K≥L циклов тестирования, каждый из которых начинается с нового псевдослучайного числа. Известно также [3], что чем меньше L величины P, тем чаще в тестируемое ОЗУ будут записываться одинаковые L-разрядные двоичные числа. Это ведет к тому, что в такой ситуации эффективность обнаружения неисправностей, обусловленных информационным взаимовлиянием элементов памяти, еще более снижается, так как доля нулевых значений в отрезках псевдослучайных двоичных последовательностей может существенно отличаться от 0,5.

Недостатком данного способа тестирования ОЗУ является плохо прогнозируемая его эффективность по обнаружению неисправностей, обусловленных информационным взаимовлиянием элементов памяти и неопределенность выбора достаточного количества циклов тестирования в зависимости от организации тестируемого ОЗУ.

Изобретение направлено на обеспечение одинаковой и прогнозируемой эффективности обнаружения константных неисправностей и неисправностей, обусловленных информационным взаимовлиянием элементов памяти, в ОЗУ с произвольной организацией.

Это достигается тем, что структуру циклического регистра сдвига первоначально определяют на основе следующей системы неравенств

M=(2^P-1)≥N*L, К≥int[Log₂(N*L)+0.5],

где int[X] - целая часть X,

а затем в процедуру генерации тестовых псевдослучайных чисел дополнительно вводят операцию селекции, где из подряд формируемых псевдослучайных чисел в качестве тестовых выбирают только те, которые отстоят друг от друга точно на L псевдослучайных чисел по следующей зависимости

,

j - номер ячейки ОЗУ,

H_j - номер псевдослучайного числа, записываемого в j-ю ячейку ОЗУ.

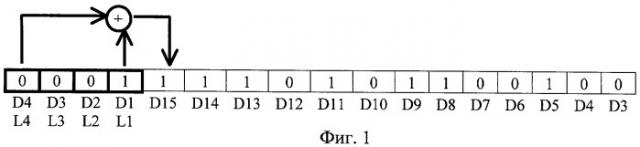
На фиг.1 представлен 4-разрядный генератор псевдослучайной двоичной последовательности (т.е. P=4), период повторения которого M=2^P-1=15 и который реализован на циклическом регистре сдвига с сумматором по модулю 2 в цепи обратной связи. Порождающий псевдослучайную последовательность полином имеет следующий вид 1+X+X⁴ и, следовательно, определяет условие подключения к входам сумматора по модулю 2 выходов первого (D1) и четвертого (D4) разрядов циклического регистра сдвига. На этой же фиг.1 показана сама псевдослучайная последовательность в развернутом виде.

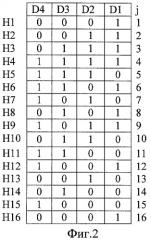
На фиг.2 показана последовательность 4-разрядных двоичных псевдослучайных чисел, которая формируется по способу-прототипу в случае тестирования ОЗУ с организацией L=P и N≈2^P, т.е. с организацией 16 ячеек памяти по 4 разряда.

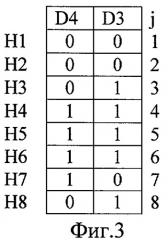
На фиг.3 показана последовательность 2-разрядных двоичных псевдослучайных чисел, которая формируется по способу-прототипу в случае тестирования ОЗУ с организацией L=2 и N=8, т.е. с организацией 8 ячеек памяти по 2 разряда.

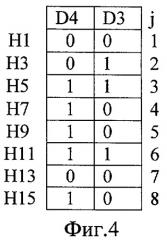
На фиг.4 показана последовательность 2-разрядных двоичных псевдослучайных чисел, которая формируется по заявляемому способу в случае тестирования ОЗУ с организацией L=2 и N=8, т.е. с организацией 8 ячеек памяти по 2 разряда.

Как видно на фиг.2, при подряд формируемых тестовых и эталонных псевдослучайных чисел по способу-прототипу и при условии, что 2^P=N и L=P в одноименных разрядах ОЗУ формируются одни и те же псевдослучайные двоичные последовательности, но сдвинутые относительно друг друга на один или более шагов.

Однако, как видно на фиг.2, между парами элементов памяти, расположенных симметрично главной диагонали (элементы H1D3-H2D4, H1D2-H3D4, H1D1-H4D4), способ-прототип не обеспечивает их «бинарный антагонизм», так как в эти парные элементы записываются одинаковые данные. То же самое наблюдается между элементами памяти, расположенными симметрично относительно всех других диагоналей, параллельных главной диагонали.

Как видно на фиг.3, при подряд формируемых тестовых и эталонных псевдослучайных чисел по способу-прототипу и при условии, что 2^P>N и L<P, в одноименных разрядах ОЗУ формируются лишь отрезки одной и той же псевдослучайной двоичной последовательности, но сдвинутые относительно друг друга на один или более шагов. При этом чем меньше L величины Р, тем чаще в тестируемое ОЗУ будут записываться одинаковые двоичные числа.

Как видно на фиг.4, при формировании тестовых и эталонных псевдослучайных чисел по заявляемому способу, они отстоят друг от друга на L=2 псевдослучайных чисел. Необходимо выполнение условия L*N≤2^P-1. Тогда при такой записи псевдослучайных чисел в последовательные ячейки ОЗУ в них будет записана используемая псевдослучайная двоичная последовательность. Это видно на фиг.4, при следующем порядке обхода двоичных элементов: (H1D4), (H1D3), (H3D4), (H3D3), (H5D4), (H5D3), (H7D4), (H7D3), (H9D4), (H9D3), (H11D4), (H11D3), (H13D4), (H13D3), (H15D4), (H15D3). Данный порядок формирования тестовых и эталонных псевдослучайных чисел гарантирует максимизацию эффективности обнаружения всех константных неисправностей и неисправностей, обусловленных информационным взаимовлиянием элементов памяти в многоразрядном ОЗУ с произвольной организацией за К=int[Log₂(N*L)+0.5] полных циклов тестирования. Для этого достаточно удовлетворить условие L*N≤2^P-1, где N - количество ячеек памяти ОЗУ, а P - степень полинома, порождающего псевдослучайную последовательность.

Техническим результатом от использования заявляемого изобретения является обеспечение одинаковой и прогнозируемой эффективности обнаружения константных неисправностей и неисправностей, обусловленных информационным взаимовлиянием элементов памяти, в ОЗУ с произвольной организацией за К=int[Log₂(N*L)+0.5] полных циклов тестирования при выполнении условия L*N≤2^P-1, где N - количество ячеек памяти ОЗУ, а P - степень полинома, порождающего псевдослучайную последовательность.

Источники информации:

1. Владимирский М.М. Тестирование ОЗУ с помощью псевдослучайной двоичной последовательности. «Микропроцессорные средства и системы», №4, 1990. - С.91-92.

2. Акинина Ю.С., Тюрин СВ. Об одном подходе к формализации понятий «необходимость» и «достаточность» функциональных тестов ОЗУ // Вестник ВГТУ. Научно-технический журнал. Выпуск 8.1 Воронеж, 2001 г. - С.50-52.

3. Мухачев Л.Ф., Попова В.И., Тюрин С.В. Генератор пуассоновского потока импульсов // Приборы и техника эксперимента, №2, 1984. - С.106-108.

Способ тестирования ОЗУ путем использования Р-разрядного генератора псевдослучайных чисел на основе циклического регистра сдвига с линейной обратной связью и периодом повторения М, структуру которого предварительно определяют на основе системы неравенствР≥L, М=(2^Р-1)≥N,K≥L,где L - разрядность тестируемого ОЗУ;N - количество ячеек тестируемого ОЗУ, заключающийся в том, что проводят подряд не менее К циклов тестирования, в каждом из которых выполняют, последовательно чередуя, процедуру записи тестовых L-разрядных псевдослучайных чисел во все N ячейки ОЗУ, а затем процедуру чтения из каждой ячейки ОЗУ записанных в них данных и сравнения их с тестовыми псевдослучайными числами, причем для формирования тестовых псевдослучайных чисел сначала в генератор псевдослучайных чисел записывают новое начальное двоичное Р-разрядное число, отличное от нуля, L-разрядов которого позже используют как первое тестовое число, затем последовательно осуществляют (N-1) циклических сдвигов в регистре сдвига с линейной обратной связью, и таким образом формируют все N L-разрядные тестовые числа, отличающийся тем, что структуру циклического регистра сдвига первоначально определяют на основе следующей системы неравенствМ=(2^P-1)≥N·L, K≥int[Log₂(N·L)+0.5],где int[X] - целая часть X,а затем в процедуру генерации тестовых псевдослучайных чисел дополнительно вводят операцию селекции, где из подряд формируемых псевдослучайных чисел в качестве тестовых выбирают только те, которые отстоят друг от друга точно на L псевдослучайных чисел по следующей зависимости j - номер ячейки ОЗУ,H_j - номер псевдослучайного числа, записываемого в j-ю ячейку ОЗУ.