Способ организации вычислений суммы n m-разрядных чисел

Способ организации вычислений суммы n m-разрядных чисел

Иллюстрации

Показать все

Реферат

Изобретение относится к вычислительной технике и предназначено для построения быстродействующих многооперандных параллельно-конвейерных сумматоров, для обработки массивов целых положительных чисел.

Известен итерационный способ суммирования массива целых положительных чисел, при котором первое m-разрядное слагаемое суммируется со вторым m-разрядным слагаемым, затем полученная сумма суммируется с третьим m-разрядным слагаемым и так далее, пока не будет получена (m-поразрядная искомая сумма. Недостаток состоит в том, что, во-первых, при итерационном способе суммирования чисел выполняется n-1 операций суммирования, а с учетом последовательного способа последовательного способа переносов в старшие разряды - количество тактов суммирования равно (m-1)·n. Во-вторых, процесс формирования суммы является последовательным процессом.

Техническим результатом от использования способа организации вычислений суммы n m-разрядных чисел является повышение скорости вычисления за счет замены серии из n арифметических операций сложения m параллельно исполняемыми операциями подсчета количества единичных бит в разрядных срезах, формируемых из разрядов суммируемых чисел. На основании анализа и модификации полученных значений сумм количества единиц во всех разрядных срезах выполняется формирование значения двоичного числа, являющегося значением искомой суммы. В результате количество тактов необходимых для формирования значения суммы массива целых двоичных чисел будет равно (log₂n)·m тактов. Таким образом, предлагаемый способ обеспечивает выполнение операции формирования суммы массива n m-разрядных чисел быстрее известного итерационного способа в ((m-1)·n)/((log₂n)·m) раз, например, при m=100, n=64 вычисления будут выполняться в 8 раз быстрее.

Описание работы устройства: каждое i-oe двоичное позиционное слагаемое можно представить в виде последовательности бит A_i(a_m, a_m-1, …, a₂, a₁), где m-разрядность числа, i∈[1, n]. Тогда n слагаемых можно представить в виде матрицы:

( a 1, m , a 1, m − 1 ,   … , a 1,1 a 2, m , a 2, m − 1 ,   … , a 2,1 … a n , m , a n , m − 1 ,   … , a n ,1 )

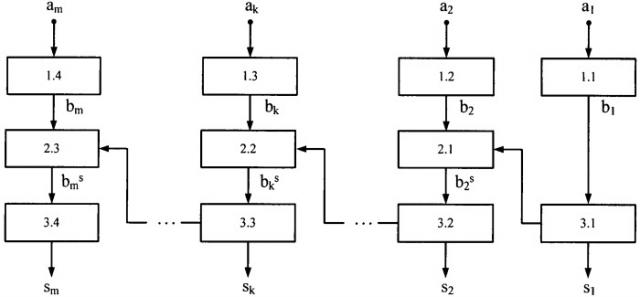
Способ организации конвейерных вычислений суммы n m-разрядных чисел заключается в параллельном подсчете количества единиц в m двоичных векторах, являющихся столбцами приведенной выше матрицы. В результате формируется m двоичных чисел b_i - значений количества единиц в соответствующих n-разрядных векторах, где i∈[1, m].

Младший разряд числа b₁ является первым разрядом s₁ искомой суммы, затем выполняется сдвиг первого двоичного числа b₁ на один разряд вправо, после чего полученный результат суммируется с числом b₂, младший разряд полученной суммы b 2 s является вторым разрядом s₂ суммы n m-разрядных исходных чисел.

Затем выполняется сдвиг двоичного числа b 2 s на один разряд вправо, после чего полученный результат суммируется с числом b₃, младший разряд полученной суммы b 3 s является третьим разрядом s₃ суммы n m-разрядных исходных чисел. И так далее вычисления продолжаются аналогичным образом до вычисления суммы b k s , младший разряд которой является k-м разрядом s_k суммы n m-разрядных исходных чисел.

Затем выполняется сдвиг двоичного числа b k s на один разряд вправо, после чего полученный результат суммируется с числом b_k+1, младший разряд полученной суммы b k + 1 s является (k+1)-м разрядом s_k+1 суммы n m-разрядных исходных чисел. И так далее вычисления продолжаются аналогичным образом до вычисления суммы b m − 1 s , младший разряд которой является (m-1)-м разрядом S_m-1 суммы n m-разрядных исходных чисел.

Затем выполняется сдвиг двоичного числа b m − 1 s на один разряд вправо, после чего полученный результат суммируется с числом b_m, младший разряд полученной суммы b m s является m-м разрядом s_m суммы n m-разрядных исходных чисел.

Затем выполняется сдвиг двоичного числа b m s на один разряд вправо, и в случае, если b m s = 0 , то вычисление прекращается, иначе младший разряд является s_m+1-м разрядом суммы n m-разрядных исходных чисел.

если b m s ≠ 0 , то выполняется сдвиг двоичного числа b m s и полученное число является значениями старших разрядов искомой суммы, начиная с m+1 разряда искомой суммы. В итоге через m тактов сдвига будет сформирована сумма n m-разрядных исходных чисел - число s₁, s₂, …, s_k, …, s_m.

Пример: необходимо сложить четыре (m=4) трехбитных (n=3) операнда: a₁=111, а₂=101, а₃=001, а₄=111. Запишем их в виде матрицы с элементами a_i,j

( 111 101 001 111 )

Параллельно подсчитывается число единиц в столбцах матрицы: b₁=100, b₂=010, b₃=011. Так как младший бит b₁ равен нулю, то бит результата s₁=0.

Число b₁ сдвигается на один разряд вправо и результат сдвига b 1 ' = 010 суммируется с числом b₂=010. Сумма b 2 s = 100 , ее младший разряд является вторым битом результата s₂=0.

Число b 2 s сдвигается на один разряд вправо и результат сдвига b 2 s ' = 010 суммируется с числом b₃=011. Сумма b 3 s = 101 , ее младший разряд является третьим битом результата s₃=1.

Число b 3 s сдвигается на один разряд вправо и младший разряд результата сдвига b 3 s ' = 010 является четвертым битом результата s₄=0. Так как b 3 s ' не равно нулю, то сдвиг повторяется: b 3 s ' ' = 001 , младший бит является пятым битом результата s₅=1. Так как b 3 s ' ' не равно нулю, то сдвиг повторяется: b 3 s ' ' ' = 000 , после чего операция прекращается, так как b 3 s ' ' ' равно нулю. В итоге получена искомая сумма (s_3,3, s_3,2, s_3,1, s_2,1, s_1,1)=10100.

Если принять за время суммирования пары n-разрядных чисел n тактов работы устройства, то время вычисления суммы в устройстве на базе описанного способа равно p-m тактов, где p=log₂n, в то время как время суммирования итерационным способом равно m·n тактов. Таким образом, быстродействие устройства на базе описанного способа в n/(log₂n) раз выше по сравнению с быстродействием устройства на базе известного итерационного способа суммирования.

Примером построения устройства на базе способа организации вычислений суммы n m-разрядных чисел может служить ее программирование на программируемых логических интегральных схемах (ПЛИС).

На фигуре представлен вариант структурной схемы устройства, реализующего способ организации вычислений суммы n m-разрядных чисел в общем виде, где 1 - счетчик единичный бит в двоичных векторах, 2 - p-разрядный двухплечевой сумматор, где p=log₂n, 3 - сдвиговый p-разрядный регистр, a₁-a_n - m-разрядные информационные входы схемы, s₁-S_m - одноразрядные информационные выходы схемы, b₁-b_m - р-разрядные выходы счетчиков 1, b 1 s − b m s − ( p + 1 ) - разрядные выходы сумматоров 2.

Способ суммирования n m-разрядных целых положительных двоичных чисел в позиционной системе счисления в суммирующем устройстве, заключающийся в том, что в суммирующем устройстве параллельно выполняется подсчет количества единиц в m n-разрядных двоичных векторах, составленных из первых разрядов n чисел, вторых разрядов n чисел, …, k-х разрядов n чисел, …, m-х разрядов n чисел; в результате параллельного подсчета количества единиц в m двоичных векторах формируется m двоичных чисел - значений количества единиц в соответствующих n-разрядных векторах, причем первое двоичное число b₁ - значение количества единиц в первом n-разрядном векторе, второе двоичное число b₂ - значение количества единиц во втором n-разрядном векторе, …, k-e двоичное число b_k - значение количества единиц в k-м n-разрядном векторе, …, m-е двоичное число b_m - значение количества единиц в m-м n-разрядном векторе; младший разряд числа b₁ является первым разрядом s₁ суммы n m-разрядных исходных чисел; затем выполняется сдвиг двоичного числа b₁ на один разряд вправо, после чего полученный результат суммируется с числом b₂, где младший разряд полученной суммы b 2 s является вторым разрядом s₂ суммы n m-разрядных исходных чисел; затем выполняется сдвиг двоичного числа b 2 s на один разряд вправо, после чего полученный результат суммируется с числом b₃, младший разряд полученной суммы b 3 s является третьим разрядом s₃ суммы n m-разрядных исходных чисел и так далее вычисления продолжаются аналогичным образом до вычисления суммы b k s , где младший разряд которой является k-м разрядом s_k суммы n m-разрядных исходных чисел; затем выполняется сдвиг двоичного числа b k s на один разряд вправо, после чего полученный результат суммируется с числом b_k+1, младший разряд полученной суммы b k + 1 s является (k+1)-м разрядом s_k+1, суммы n m-разрядных исходных чисел и так далее вычисления продолжаются аналогичным образом до вычисления суммы b m − 1 s , где младший разряд которой является (m-1)-м разрядом s_m-1 суммы n m-разрядных исходных чисел; затем выполняется сдвиг двоичного числа b m − 1 s на один разряд вправо, после чего полученный результат суммируется с числом b_m, младший разряд полученной суммы b m s является m-м разрядом s_m суммы n m-разрядных исходных чисел; затем выполняется сдвиг двоичного числа b m s на один разряд вправо, и в случае, если b m s = 0 , то вычисление прекращается, иначе младший разряд является s_m+1-м разрядом суммы n m-разрядных исходных чисел; если b m s ≠ 0 , то выполняется сдвиг двоичного числа b m s и полученное число является значениями старших разрядов искомой суммы, начиная с m+1 разряда искомой суммы; в итоге через m тактов сдвига будет сформирована сумма n m-разрядных исходных чисел - число s₁, s₂, …, s_k, …, s_m.