Устройство для определения знака модулярного числа

Устройство для определения знака модулярного числа

Иллюстрации

Показать все

Реферат

Изобретение относится к вычислительной технике и может быть использовано для определения знаков модулярных чисел, входящих в вычислительные устройства, функционирующие в системе остаточных классов. Известно устройство, для определения знаков числа, представленное в системе остаточных классов (А.С. № 1552181, БИ №11, 1990), состоящее из блока 1 определения номера интервала, схем 3 и 4 сравнения, элементов «или» 5 и 6. Однако данное устройство обладает следующими недостатками: низкое быстродействие и большие аппаратные затраты. Наиболее близким по технической сущности к заявленному устройству является устройство для определения знака числа, представленного в системе остаточных классов (А.С. № 1674121, БИ №32, 1991), содержащее блок определения номера интервала, схемы сравнения, группы шифрования и дешифрования, сумматор и логические элементы «или».

Недостатками известного устройства являются малая скорость определения знака числа и большие аппаратные затраты.

Целью настоящего изобретения является повышение быстродействия и сокращение аппаратных затрат.

Поставленная цель достигается тем, что в известном устройстве введены просмотровые таблицы (LUT) и параллельный сумматор.

Рассмотрим метод определения знака числа, обладающий высоким быстродействием и низкими затратами оборудования. Суть метода быстрого определения знака модулярного числа основан на использовании китайской теореме об остатках числа, которая связывает позиционное число А с его представлениями в остатках (α₁, α₂, …, α_n), где α_i наименьшие неотрицательные остатки числа по модулям p₁, p₂, …, p_n.

Цифры α_i данного представления по выбранным модулям образуются следующим образом

где - целочисленное частное, p_i - основания (модули) - взаимно-простые числа. В теории чисел доказано, что если ∀i≠j(p_i, p_j)=1, то представление (1) является единственным, при условии 0≤A<P, где - диапазон представления чисел, то есть существует число A, для которого:

Известна Китайская теорема об остатках, которая связывает позиционное число А с его представлением в остатках (α₁, α₂,…,α_n), где α_i - наименьшие неотрицательные вычеты числа, относительно модулей системы остаточных классов p₁, p₂, …, p_n следующим выражением

где , p_i - модули СОК, - мультипликативная инверсия P_i относительно p_i, и .

Если (3) разделить на константу P, то получим приближенное значение

где - константы выбранной системы, а α_i - разряды числа, представленного в СОК, при этом значение каждой суммы будет в интервале [0, 1). Конечный результат суммы определяется после суммирования и отбрасывания целой части числа с сохранением дробной части суммы. Дробная часть может быть записана также как Amod1, потому что . Количество разрядов дробной части числа определяется максимально возможной разностью между соседними числами. При необходимости точного сравнения необходимо вычислить значение (4), которое является эквивалентом преобразования из СОК в позиционную систему счисления. Для решения задач основных процедур принятия решения достаточно знать приблизительно значения чисел A и B по отношению к динамическому диапазону P, которое выполняется достаточно просто, но при этом правильно определяет соотношение A=B, A>B или A<B.

Рассмотрим случай, когда рабочий диапазон разбит на два интервала - положительные числа, и - отрицательные числа.

Известно, что при кодировании дополнительным кодом, отрицательная часть динамического диапазона находится у верхнего предела полного диапазона. Положительные числа из дополнительного диапазона отображаются на область при нечетных P и на область при четных P. Отображение динамического диапазона на соответствующую область для избыточного кода СОК показано на рисунке 1.

Это обстоятельство может привести к ошибке сравнения, так как отрицательные числа попадают в верхнюю часть полного диапазона, и все отрицательные числа будут давать ошибки, что не соответствует действительности в силу разнесения динамического диапазона.

Для преодоления этой трудности необходимо произвести сдвиг отрицательной области путем вращения остаточного кольца в положение, указанное на рисунке 2. Пунктиром показана область, которая перенесена в начало диапазона.

В результате отрицательные числа будут отображены в начальной части динамического диапазона.

Показанное на рисунке 2 вращение, называется сдвигом полярности и его можно осуществить путем прибавления перед сравнением модулярных чисел константы при нечетном P или при четных P к каждому .

Если , то сдвиг полярности в пределах СОК оказывается простым остатком, определяемом по формуле , в которой α_ic обозначает остаточные цифры после сдвига полярности.

Рассмотренный метод определения такой позиционной характеристики модулярного кода, как определение знака числа, показал, в отличие от известных, простоту его вычисления, так как для его реализации не используется вычисление коэффициентов ОПСС, которое требует больших аппаратных и временных затрат. По этой причине данный метод представляет собой особую важность и является одним из лучших решений на настоящее время. Перечисленные операции являются важнейшими для машинной модулярной арифметики и их применение может дать значительные преимущества не только в таких приложениях, в которых основная доля вычислений приходится на точное умножение, возведение в степень больших чисел в сочетании со сложением и вычитанием, но и в которых довольно часто появляется необходимость сравнения и определения знака числа. Известно, что теорема кодирования Сабо гласит, что нет лучших методов определения позиционных характеристик, при которых не используется их однозначность, чем перевод чисел из СОК в ОПСС, поскольку величины числа в модулярном представлении существенным образом зависят от всех остатков числа. Однако проведенные исследования по определению приблизительных характеристик, которые решают задачу формирования конструкций сравнения, не отвечают утверждению указанной теоремы Сабо. Таким образом можно сделать вывод о том, что теорема Сабо работает только при точных методах.

Для повышения эффективности обработки данных в модулярной арифметике рассмотрим приложения приблизительных методов для определения знака числа.

Определение знака модулярных чисел

Известно, что для определения знака числа используются номера интервалов, в которых расположено число, что позволяет получить оценку исследуемого числа по его величине с точностью до величины интервала. Числовой диапазон P может быть разбит на p_i интервалов величиной

В качестве второго машинного нуля выбирается точка числового диапазона . Числа, расположенные в поддиапазонах и считаются числами разных знаков.

Если дано представление (α₁, α₂,…,α_n), то для того чтобы установить знак числа, которое оно представляет, достаточно решить задачу о принадлежности этого числа к определенному интервалу. В случае если p_i=2 достаточно решить задачу о принадлежности этого числа к первой или второй половине диапазона . Эта задача решается сравнением данного представления с представлением , при условии, что p₁=2. Все известные методы реализуют данный алгоритм на основе использования абсолютных величин, здесь же мы предлагаем использовать относительные величины, что существенно упрощает преобразование, сохраняя при этом основные функциональные возможности.

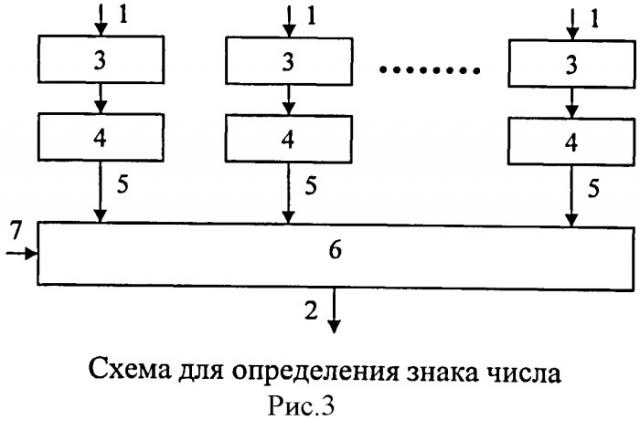
На рисунке 3 приведена схема устройства для определения знака модулярного числа по модулям p₁, p₂, …, p_n.

Устройство состоит из входных регистров 3 по модулям p₁, p₂, …, p_n, для временного хранения разрядов СОК (каждый разряд СОК представлен двоичным кодом), просмотровых таблиц (LUT) для хранения произведения констант разрядов СОК. , где мультипликативная инверсия, p_i - модуль СОК, , , параллельного сумматора для суммирования входных шин 1 для подачи исходного числа, выходной шины для фиксирования знака числа и входа .

Работа устройства для определения знака модулярного числа определяется следующим образом.

На входные регистры (RGi) 3 по входам 1 устройства для определения знака числа подается исходное число, представленное в системе остаточных классов A=(α₁, α₂,…,α_n). На выходе 2 формируется знак модулярного числа. Выходы регистров являются адресными входами просмотровых таблиц (LUT) (память), в элементах которых хранятся значения . С выходов 5 просмотровых таблиц 4 выбранные значения поступают на первые входы сумматора, а на второй вход 7 поступает значение . Результатом операции является знак числа 0 - положительное, 1 - отрицательное.

Код числа A, для которого необходимо определить интервал, что равносильно определению знака числа, поступает на входные регистры RG_i в двоичном коде (каждый разряд СОК кодируется двоичным кодом). Сигналы с выходов регистров поступают на входы просмотровых таблиц LUT. В просмотровых таблицах хранятся произведения констант k_i и остатков α_i, то есть , представленных в естественной форме двоичной дроби в дополнительном коде. Количество элементов памяти (N) просмотровых таблиц определяется выражением .

Выходные сигналы просмотровых таблиц в дополнительном двоичном коде поступают на вход сумматора, в котором уже записана константа 0,5 во время начальной установки. (Дополнительный код используется для того, чтобы операцию вычитания заменить операцией сложения). Знак результата сложения определяет интервал: первый или второй, что соответственно определяет знак числа.

Пример 4. Пусть дана система оснований p₁=2, p₂=3, p₃=5, p₄=7. Тогда P=210. Константы k_i соответственно равны k₁=0,5, k₂≈0,3333, k₃=0,6, k₄≈0,5714.

Дано число A=(1, 1, 2, 0). Требуется определить знак числа A.

Решение. В регистры RG₁=1, RG₂=1, RG₃=2, RG₄=0. В соответствии с этими значениями регистров (адресные входы LUT) на выходах которых формируются значения LUT₁=0,5, LUT₂=0,3333·1=0,3333, , LUT₄=0.

Таким образом, при суммировании в знаковом разряде сумматора будет 0, что говорит о том, что число находится в первом интервале, поэтому , то есть число A - положительное.

Определение знака осуществляется за n суммировании, где n - число оснований (модулей) СОК. Время суммирования определяется логической глубиной устройства (количество последовательно соединенных элементов) и временем суммирования сумматора. Для уменьшения времени суммирования, схему сумматора можно реализовать по принципу дерева (рекурсивного сдваивания). Кроме того реализация сумматора может быть выполнена на искусственных нейронных сетях.

Устройство для определения знака модулярного числа, отличающееся тем, что в него введены входные регистры по модулям p₁, p₂, …, p_n, для временного хранения разрядов СОК, параллельный сумматор для суммирования , входные шины для подачи исходного числа, просмотровые таблицы для хранения произведений констант разрядов СОК , представленных в двоичном коде, на входы которых поступают с выхода регистров двоичные коды разрядов СОК α_i, выходы которых соединены с входами сумматора, на вторые входы которого поступает константа , выход которого является выходом устройства.