Способ определения параметра оптической анизотропии сигма материала кубического монокристалла, относящегося к классу симметрии m3m, или 432

Способ определения параметра оптической анизотропии сигма материала кубического монокристалла, относящегося к классу симметрии m3m, или 432

Иллюстрации

Показать все

Реферат

Изобретение относится к области измерительной техники и может быть использовано для определения параметра оптической анизотропии кубических кристаллов, относящихся к классу m3m, 4 ¯ 3 m или 432 симметрии.

В активных элементах твердотельных лазеров неизбежно возникают тепловые потери, которые приводят к таким негативным эффектам, как возникновение тепловой линзы и термонаведенной деполяризации излучения. Термонаведенная деполяризация в активных элементах является одним из главных факторов, сдерживающих увеличение средней мощности твердотельных лазеров. Термонаведенное двулучепреломление, вызванное в активных элементах фотоупругим эффектом, приводит к тому, что исходно оптически изотропная среда - стекло, кубический кристалл или керамика из кубического кристалла - становится анизотропной. Термонаведенные собственные поляризации линейны и ортогональны друг другу, однако различны в различных точках поперечного сечения образца. В стекле они направлены вдоль и поперек градиента температуры, в кристалле и керамике устроены более сложно. Разность фаз термонаведенного двулучепреломления также является функцией поперечных координат. В результате изначально поляризованное излучение после прохождения образца становится деполяризованным.

Под деполяризованным излучением понимается излучение, у которого поляризация постоянна во времени, но изменяется от точки к точке поперечного сечения. Под распределением локальной степени деполяризации излучения Г понимается отношение интенсивности деполяризованной компоненты излучения к суммарной интенсивности излучения в двух поляризациях в каждой точке поперечного сечения. Интегрирование распределения Г по поперечному сечению с учетом формы пучка, либо измерение отношения мощности в деполяризованной компоненте к суммарной мощности в двух поляризациях дает величину интегральной степени деполяризации излучения γ.

Негативные последствия термонаведенного двулучепреломления очевидны. Прежде всего, это потери мощности, равные степени деполяризации в поляризованном излучении. Кроме того, исходное поляризованное излучение получает в процессе прохождения активного элемента амплитудную (например, «мальтийский крест») и фазовую (например, астигматизм) модуляцию, связанную с тем, что распределение локальной степени деполяризации существенно неоднородно по поперечному сечению. Таким образом, вызванные двулучепреломлением потери мощности в исходной пространственно-поляризационной моде, например, в линейно-поляризованном гауссовом пучке, заметно больше, чем интегральная степень деполяризации γ.

Впервые параметр ξ (stress-optic anisotropy ratio) был введен в работе R.E.Joiner, J.Marburger, and W.H.Steier, Applied Physics Letters 30,485 (1977) как

ξ = π 44 π 11 − π 12                      (1)

где π_ij(ij=1,2…6) - пьезооптические коэффициенты, т.е. элементы пьезооптического тензора в двухиндексном обозначении Ная. В этой же работе было показано, что если ξ<0, то в условиях плоско-напряженного состояния (например, в тонком диске) существует такая ориентация кристалла, в которой термонаведенная деполяризация зануляется.

В статье Л.Н.Соме, А.А.Тарасов. Квантовая электроника 6, 2546 (1979) были получены аналитические выражения для деполяризации в длинных цилиндрических кристаллах с ориентацией [001] и был введен параметр

ξ p = 2 p 44 p 11 − p 12 ,                  (2)

который позднее в книге А.В. Мезенов, Л.Н. Соме, А.И. Степанов. Термооптика твердотельных лазеров (Машиностроение, Ленинград, 1986) был назван параметром оптической анизотропии ξ_р. Здесь p_ij(i,j=l,2…6) - элементы упругооптического тензора в обозначении Ная (фотоупругие коэффициенты).

Практически во всех работах, посвященных тепловым эффектам в кубических кристаллах, пренебрегается анизотропией тензора упругости. В этом случае параметры ξ_p и ξ тождественно равны друг другу. В кристаллах с ориентацией [001] в случае осесимметричного тепловыделения и в приближении длинного цилиндра, если использовать параметр оптической анизотропии, записанный через пьезооптические коэффициенты, упругая анизотропия кристалла никак не скажется на выражениях для термонаведенной деполяризации. Заметим, что для всех стекол ξ=1.

Задача о термонаведенной деполяризации при произвольной ориентации кубического кристалла с симметрией 432, 4 ¯ 3 m и m3m аналитически решена в статье Е.Khazanov, N.Andreev, О.Palashov, A.Poteomkin, A.Sergeev, О.Mehl, and D.Reitze, Applied Optics 41, 483 (2002). В ней получены аналитические выражения для разности фаз термонаведенного двулучепреломления δ и направления собственных поляризаций Ψ при произвольной ориентации кристалла при любом аксиально-симметричном распределении плотности мощности тепловыделения, и показано, что они зависят от ориентации кристалла (углы Эйлера α и β), от угла между направлением поляризации лазерного излучения и одной из кристаллографических осей θ, от профиля источника тепловыделения, от отношения радиуса кристалла и радиуса источника тепла, от полярных координат r и φ, от нормированной мощности источника тепловыделения p

p = P h λ α T к n 0 3 4 1 + υ 1 − υ ( p 11 − p 12 ) ,            (3)

и от параметра оптической анизотропии кристалла ξ. Здесь υ - коэффициент Пуассона, α_Т - коэффициент теплового расширения, к - теплопроводность, n₀ - "холодный" показатель преломления, p_ij(i,j=1,2…6) - элементы тензора фотоупругости в двухиндексном обозначении Ная (фотоупругие коэффициенты), P_h - мощность тепловыделения.

Важно отметить, что из материальных констант среды все, кроме ξ, (а именно, к, α_T, n₀, υ и p_ij) входят только в нормированную мощность тепловыделения p (3), от которой δ зависит линейно, а Ψ не зависит вообще. Другими словами, увеличение к или уменьшение α_T позволяет пропорционально увеличить мощность тепловыделения Д при любых r и φ, при любой ориентации кристалла и т.д. В то же время, от параметра оптической анизотропии ξ сложным образом зависят и δ, и Ψ. В частности, выбор оптимальной ориентации существенно зависит от ξ.

В статье показано, что параметр оптической анизотропии ξ является универсальным для любой ориентации и единственной характеристикой среды, влияющей на зависимость термонаведенного двулучепреломления от ориентации кристалла. В частности, выражения для δ и Ψ для ориентации [111] могут быть получены из выражений для ориентации [001] с помощью формальной замены

ξ → 1 и p → p ( 1 + 2 ξ ) / 3                   (4)

Построена также теория тепловых эффектов в лазерной керамике (см., например, 5. Е.A.Khazanov, Optics Letters 27, 716 (2002); М.А.Каган and Е.А.Хазанов, Квантовая электроника 33, 876 (2003); И.Л.Снетков, И.Б.Мухин, О.В.Палашов и Е.А.Хазанов, Квантовая электроника 37, 633 (2007)). Теория учитывает, что ориентация кристаллографических осей (а следовательно, и осей термонаведенного двулучепреломления) в каждом зерне случайна.

В работах I.В.Mukhin, О.V.Palashov, Е.A.Khazanov, A.Ikesue, and Y.L.Aung, Optics Express 13, 5983 (2005); A.A.Soloviev, I.L.Snetkov, V.V.Zelenogorsky, I.E.Kozhevatov, О.V.Palashov, and E.A.Khazanov, Optics Express 16, 21012 (2008) приведены примеры экспериментального наблюдения предсказанного теорией эффекта мелкомасштабной пространственной модуляции термонаведенной деполяризации и волнового фронта пучка, прошедшего через керамику. Этот эффект присущ исключительно керамике, он не имеет аналога ни в стеклах, ни в монокристаллах и определяется размером гранул и параметром ξ.

Исследование термонаведенного двулучепреломления в изоляторах Фарадея показало, что параметр ξ сохраняет свою универсальность и уникальность в магнитооптических средах (см. Е.Khazanov, N.Andreev, О.Palashov, A.Poteomkin, А.Sergeev, О.Mehl, and D.Reitze, Applied Optics 41,483 (2002)), в том числе и керамических (см. М.A.Kagan and Е.A.Khazanov, Applied Optics 43,6030 (2004)).

Параметр оптической анизотропии £ является определяющим не только для стержневой геометрии, но также для дисков (см. работы А.В.Мезенов, Л.Н.Соме, А.И.Степанов. Термооптика твердотельных лазеров (Машиностроение, Ленинград, 1986); И.Б. Мухин, Е.А.Хазанов, Квантовая электроника 34, 973 (2004); А.А.Соловьев, И.Л.Снетков, Е.А. Хазанов, Квантовая Электроника 39, 302 (2009); А.А.Soloviev, I.L.Snetkov, Е.А.Khazanov, Quantum Electronics 39, 302 (2009); B.M.Митькин, О.С.Щавелев, Оптико-механическая промышленность 9, 26 (1973)) и слэбов (см. работы А.В.Мезенов, Л.Н.Соме, А.И.Степанов, Термооптика твердотельных лазеров (Машиностроение, Ленинград, 1986); Е.М.Дианов, Краткие сообщения по физике 8,67 (1971)). Заметим также, что ξ определяет не только деполяризацию, но и астигматизм тепловой линзы (А.В.Мезенов, Л.Н.Соме, А.И.Степанов, Термооптика твердотельных лазеров (Машиностроение, Ленинград, 1986).

Таким образом, параметр оптической анизотропии ξ является не просто комбинацией фотоупругих коэффициентов, а характеристикой кристалла, определяющей термонаведенные поляризационные искажения в произвольно ориентированных кристаллах, а также в керамиках.

В связи с этим знание величины ξ для кристаллов, используемых в лазерах с большой средней мощностью, является принципиально важным.

Если известны элементы пьезооптического тензора π_ij, то значение ξ вычисляется по формуле (1). Для измерения π_ij требуется специальное лабораторное оборудование, отработанная методика измерения и калибровки, без которых точность измерения невелика. Из-за этого для многих кристаллов значения π_ij на нужной длине волны излучения и при необходимой температуре кристалла неизвестны, а для других в разных работах приводятся различные значения. Они могут давать различные ξ, существенно отличающиеся не только по величине, но и по знаку.

Знание величины и знака параметра оптической анизотропии является существенным при моделировании фазовых и поляризационных искажений излучения, возникающих при прохождении через термонагруженный оптический элемент, изготовленный из монокристалла или керамики. Знак параметра оптической анизотропии ξ полностью определяет оптимальную с точки зрения минимизации термонаведенных поляризационных искажений ориентацию кристалла активного элемента лазера.

Наиболее близким по технической сути к предложенному способу является метод определения параметра оптической анизотропии, основанный на непосредственном измерении интегральной степени деполяризации γ или на измерении распределения локальной деполяризации Г с последующим ее интегрированием по поперечному сечению пучка для нахождения интегральной степени деполяризации γ в кристалле с ориентацией [001], который описан в статье Е.А.Khazanov, O.V.Kulagin, S.Yoshida, D.Tanner, D.Reitze, IEEE Journal of Quantum Electronics 35, 1116 (1999) и широко использовался в других работах (Е.Khazanov, N.Andreev, О.Palashov, A.Poteomkin, А.Sergeev, О.Mehl, and D.Reitze, Applied Optics 41, 483 (2002);E.A.Khazanov, N.F.Andreev, A.N.Mal'shakov, О.V.Palashov, A.K.Poteomkin, A.M.Sergeev, A.A.Shaykin, V.V.Zelenogorsky, I.Ivanov, R.S.Amin, G.Mueller, D.B.Tanner, and D.H.Reitze, IEEE Journal of Quantum Electronics 40, 1500 (2004): Д.С.Железное, A.B. Войтович, И.Б. Мухин, O.B.Палашов, Е.А.Хазанов, Квантовая электроника 36, 383 (2006); A.V.Starobor, D.S.Zheleznov, O.V.Palashov, Е.А.Khazanov, J.Opt. Soc. Am. В 28, 1409 (2011)). При слабом двулучепреломлении (γ<<1) измеряют (находят из Г) величину интегральной степени деполяризации γ в двух положениях кристалла, когда она принимает экстремальные значения, после чего вычисляют отношение максимального и минимального значений деполяризации γmax/γmin. Как показано ранее (см. А.В.Мезенов, Л.Н.Соме и А.И.Степанов. Термооптика твердотельных лазеров. (Машиностроение, Ленинград, 1986)), γ(θ=0)=ξ²γ(θ=π/4), то есть для наблюдаемых величин γ_max/γ_min=ξ², если | ξ | > 1 и γ max / γ min = 1 / ξ 2 , если | ξ | < 1 . Следовательно, для определения ξ² нужно только знать больше или меньше единицы величина | ξ | . Если γ(θ=0)=γ_min, то | ξ | < 1 , а если γ(θ=0)=γ_max, то | ξ | > 1 . Заметим, что если положение кристаллографических осей, лежащих в плоскости торца оптического элемента, неизвестно (т.е. абсолютное значение θ неизвестно), то определить | ξ | > 1 или | ξ | < 1 можно по поведению γ при вращении кристалла вокруг оси, перпендикулярной направлениям распространения излучения и его поляризации (см. Е.Khazanov, N.Andreev, О.Palashov, A.Poteomkin, A.Sergeev, О.Mehl, and D.Reitze, Applied Optics 41,483 (2002)). Если при таком вращении оптического элемента величина γ_max не изменяется, то | ξ | > 1 , если уменьшается, то | ξ | < 1 . Таким образом, легко измерить | ξ | .

Как видно из описания, для определения | ξ | необходимо знать значение интегральной степени деполяризации γ_max в двух положениях кристалла, соответствующих γ_max и γ_min. При этом γ может быть определено из отношения мощности деполяризованной компоненты излучения к полной мощности излучения, измеренных с помощью измерителя мощности или фотоприемника, или определено по измерению распределений основной и деполяризованной компонент излучения с помощью ПЗС-камеры, которые впоследствии проинтегрированы по поперечному сечению и разделены одно на другое.

Основным недостатком способа-прототипа является то, что неопределенным остается знак ξ, способ экспериментального определения которого по термонаведенной деполяризации не был предложен ни в одной из предшествующих работ.

Задачей, на решение которой направлено настоящее изобретение, является разработка основанного на измерении термонаведенной деполяризации в оптическом элементе из кристалла с ориентацией [001], относящегося к классу симметрии m3m, 4 ¯ 3 m или 432, способа определения величины параметра оптической анизотропии ξ и его знака.

Технический результат в разработанном способе достигается тем, что, как и в способе-прототипе, измеряют распределение локальной степени деполяризации прошедшего через образец монокристалла с ориентацией [001] излучения.

Новым в первом варианте реализации способа является то, что измеряют распределения локальной степени деполяризации более чем в двух положениях кристалла; при этом по распределениям при двух положениях кристалла, в которых наблюдается максимум и минимум деполяризации, путем интегрирования этих распределений и делений одного на другое определяют величину ξ, а знак параметра ξ определяют по поведению распределения локальной степени деполяризации, представляющей собой «мальтийский крест», при равномерном повороте кристалла из положения, в котором наблюдается минимум, в положение, в котором наблюдают максимум (или наоборот) относительно направления поляризации лазерного излучения:

если при повороте кристалла вокруг оси Z на угол π/4 распределение вернулось в

исходное положение (φ₀(θ=π/4)=φ₀(θ=0)), «мальтийский крест» «колеблется», значит, ξ>0; если φ₀(θ=π/4)=φ₀(θ=0)+π/2, «мальтийский крест» «вращается», значит, ξ<0.

Новым во втором варианте реализации способа является то, что измеряют распределения локальной степени деполяризации более чем в двух положениях кристалла; при этом по распределениям локальной степени деполяризации, представляющей собой «мальтийский крест», измеряют зависимость угла наклона «мальтийского креста» φ относительно направления поляризации лазерного излучения от угла поворота кристалла θ вокруг оси, совпадающей с направлением распространения излучения, и по зависимости φ(θ), добившись максимального совпадения снятой зависимости с построенной теоретически, определяют как знак параметра ξ, так и его величину.

Способ поясняется следующими чертежами.

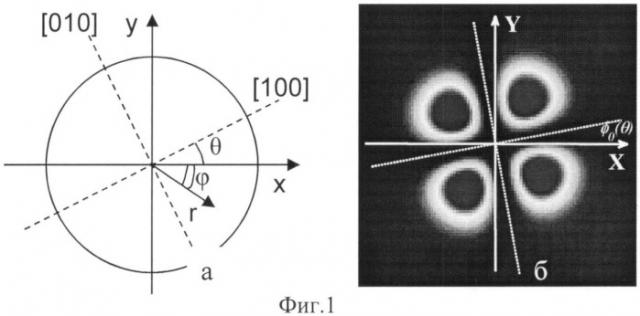
На Фиг.1 представлена геометрия кристалла (а) и распределение локальной степени деполяризации излучения, возникающее при прохождении через кристалл (б). Поляризация излучения направлена вдоль оси X, ось Z направлена перпендикулярно рисунку и совпадает с кристаллографической осью [001] и направлением распространения излучения.

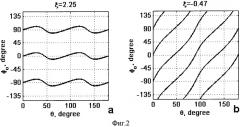
На Фиг.2 представлены зависимости φ₀(θ) для двух значений параметра ξ:(а) ξ=2,25 и (б) ξ=-0,47.

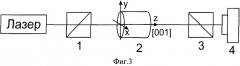
На Фиг.3 представлена принципиальная схема, с помощью которой можно осуществлять измерения распределения локальной степени деполяризации излучения. Излучение лазера является одновременно и греющим, и считывающим поляризационные искажения; 1 - поляризатор; 2 - исследуемый образец; 3 - анализатор; 4 - ПЗС камера.

Для определения величины ξ измеряют распределение локальной степени деполяризации в оптическом элементе из кристалла с ориентацией [001] в зависимости от угла θ между падающей поляризацией и одной из кристаллографических осей (Фиг.1а). Однако для определения знака ξ требуется измерять распределение локальной степени деполяризации Г(r,φ) (Фиг.1б).

Для кубических кристаллов с ориентацией [001] при осесимметричном тепловыделении в кристалле выражение для Г(r,φ) (см. А.В.Мезенов, Л.Н.Соме и А.И.Степанов, Термооптика твердотельных лазеров (Машиностроение, Ленинград, 1986); Е. Khazanov, N. Andreev, О.Palashov, A.Poteomkin, A.Sergeev, О.Mehl, and D.Reitze, Applied Optics 41,483 (2002)):

Г = sin 2 ( 2 Ψ ) sin 2 ( δ / 2 )                      (5)

где

δ = p ⋅ h ( r ) ⋅ 1 + ξ 2 tan 2 ( 2 θ − 2 ϕ ) 1 + tan 2 ( 2 θ − 2 ϕ )             tan ( 2 Ψ − 2 θ ) = ξ tan ( 2 ϕ − 2 θ ) ,                (6)

h(r) - форм-фактор, определяемый радиальной зависимостью нагрева кристалла. При слабом двулучепреломлении (δ<<1), подставляя (6) в (5), получим

Г = p 2 h 2 ( r ) 4 ( tan ( 2 θ ) − ξ tan ( 2 θ − 2 ϕ ) ) 2 ( 1 + tan 2 ( 2 θ ) ) ( 1 + tan 2 ( 2 θ − 2 ϕ ) )                (7)

Анализируя (7), легко увидеть, что распределение Г(r,φ) представляет собой так называемый «мальтийский крест» при любых θ и ξ (Фиг.1б). В то же время, направление осей симметрии креста существенно зависит от θ и ξ. Из (7) видно, что Г=0 при φ=φ₀, а φ₀ определяется выражением

tan ( 2 ϕ 0 ) = ( ξ − 1 ) tan ( 2 θ ) tan 2 ( 2 θ ) + ξ                 (8)

Исследуя функцию φ₀(θ) на экстремумы, легко показать, что экстремумы имеют место при углах θ, удовлетворяющих условию:

tan 2 ( 2 θ ) = ± ξ                  (9)

Из (9) следует, что если ξ>0, то при изменении угла θ величина угла φ₀ колеблется в интервале от минимального до максимального значения, причем амплитуда колебаний зависит от величины | ξ | . Другими словами, при вращении кристалла вокруг оси Z (изменение угла θ) «мальтийский крест» «колеблется» между двумя положениями, соответствующими двум экстремумам (Фиг.2а). Если ξ<0, то согласно (9) экстремумов функции φ₀(θ) не существует, и угол φ₀ при непрерывном изменении угла θ в пределах [0,2π] будет непрерывно меняться от 0 до 4π. «Мальтийский крест» в этом случае будет не «колебаться», а неравномерно «вращаться» с удвоенной частотой (Фиг.2б).

Таким образом, вращая кристалл с ориентацией [001] вокруг оси Z и наблюдая за «мальтийским крестом», можно однозначно определить знак ξ: если крест «колеблется», то ξ>0, а если «вращается», то ξ<0. Для стекол (ξ=1) и керамик крест будет неподвижен.

Измерив зависимость φ₀(θ) и добившись ее согласия с (8), используя ξ как подгоночный параметр, можно определить ξ.

Возможная схема измерения представлена на Фиг.3. Лазер, излучение которого используется и в качестве греющего, и в качестве зондирующего сигнала. Создание внутренних напряжений, приводящих к возникновению термонаведенной деполяризации, может быть осуществлено и другими способами: нагревом другим лазером, диодом или лампами накачки. Поляризатор 1, исследуемый образец 2, анализатор 3, скрещенный с поляризатором, и камера 4, фиксирующая распределение деполяризованной компоненты излучения.

Способ определения величины параметра оптической анизотропии ξ по первому варианту реализации осуществляют следующим образом. Для определения необходим образец исследуемого материала с кубической кристаллической решеткой, вырезанный с ориентацией [001], и известным расположением кристаллографических осей на апертуре образца.

1) Измеряют распределения локальной степени деполяризации при двух углах θ между одной из кристаллографических осей и направлением поляризации падающего излучения, равных 0 и π/4, в зависимости от мощности греющего излучения.

2) Интегрируют полученные распределения по области пучка и получают две зависимости интегральной степени деполяризации γ(θ=0) и γ(θ=π/4). Снимают зависимости γ(θ=0) и γ(θ=π/4) до такой мощности, при которой они обе выходят на квадратичную от греющей мощности зависимость. Это свидетельствует о том, что поляризационные искажения, вызванные тепловыделением, превысили холодные искажения кристалла, вызванные качеством его изготовления. При этих положениях кристалла достигаются экстремальные значения γ(θ), при этом какое из них максимум, а какое минимум определяется положением |ξ| по отношению к единице.

3) Находят отношение γ(θ=0)/γ(θ=π/4), когда они обе вышли на квадратичную зависимость от мощности тепловыделения. При этом ξ²=γ(θ=0)/γ(θ=π/4).

4) Измеряют необходимое количество распределений локальной степени деполяризации излучения при изменении угла θ от 0 до π/4 и определяют зависимость φ₀(θ). Если при повороте кристалла вокруг оси Z на угол π/4 распределение вернулось в исходное положение (φ₀(θ=π/4)=φ₀(θ=0)), это означает, что «мальтийский крест» «колеблется» и ξ>0. Если φ₀(θ=π/4)=φ₀(θ=0)+π/2, то «мальтийский крест» «вращается» и ξ<0. Необходимое количество измерений распределений локальной степени деполяризации выбирают таким, чтобы можно было однозначно определить, был ли обратный ход у «мальтийского креста» или нет.

Таким образом, предлагаемый способ в первом варианте его реализации по п.1 формулы позволяет определить величину параметра оптической анизотропии ξ и его знак.

Способ определения величины параметра оптической анизотропии ξ по второму варианту реализации осуществляют следующим образом. Для определения необходим образец исследуемого материала с кубической кристаллической решеткой, вырезанный с ориентацией [001], и известным расположением кристаллографических осей на апертуре образца.

1) Измеряют необходимое количество распределений локальной степени деполяризации при изменении угла θ от 0 до π/2 при мощности излучения, когда «отчетливо» наблюдается «мальтийский крест» (критерием может служить выход интегральной деполяризации на квадратичную зависимость от мощности падающего излучения). Необходимое количество измерений распределений локальной степени деполяризации выбирают таким, чтобы можно было однозначно определить, был ли обратный ход у «мальтийского креста» или нет.

2) По измеренным распределениям определяют экспериментальную зависимость φ₀(θ).

3) Используя формулу (8), строят теоретическую зависимость φ₀(θ) и находят как знак, так и величину ξ, соответствующую максимальному совпадению теоретической зависимости с экспериментальной (например, методом наименьших квадратов).

Таким образом, предлагаемый способ во втором варианте его реализации по п.2 формулы позволяет определить величину параметра оптической анизотропии ξ и его знак.

1. Способ определения параметра оптической анизотропии ξ материала кубического монокристалла, относящегося к классу симметрии m3m, или 432, включающий измерение распределения локальной степени деполяризации прошедшего через образец монокристалла с ориентацией [001] излучения, отличающийся тем, что измеряют распределения локальной степени деполяризации более чем в двух положениях кристалла; при этом по распределениям при двух положениях кристалла, в которых наблюдается максимум и минимум деполяризации, путем интегрирования этих распределений и делений одного на другое определяют величину ξ, а знак параметра ξ определяют по поведению распределения локальной степени деполяризации, представляющей собой «мальтийский крест», при равномерном повороте кристалла из положения, в котором наблюдается минимум, в положение, в котором наблюдается максимум (или наоборот) относительно направления поляризации лазерного излучения: если при повороте кристалла вокруг оси Z на угол π/4 распределение вернулось в исходное положение (φ₀(θ=π/4)=φ₀(θ=0)), «мальтийский крест» «колеблется», - значит, ξ>0; если φ₀(θ=π/4)=φ₀(θ=0)+π/2, «мальтийский крест» «вращается», - значит, ξ<0.

2. Способ определения параметра оптической анизотропии ξ материала кубического монокристалла, относящегося к классу симметрии m3m, или 432, включающий измерение распределения локальной степени деполяризации прошедшего через образец монокристалла с ориентацией [001] излучения, отличающийся тем, что измеряют распределения локальной степени деполяризации более чем в двух положениях кристалла; при этом по распределениям локальной степени деполяризации, представляющей собой «мальтийский крест», измеряют зависимость угла наклона «мальтийского креста» φ относительно направления поляризации лазерного излучения от угла поворота кристалла θ вокруг оси, совпадающей с направлением распространения излучения, и по зависимости φ(θ), добившись максимального совпадения снятой зависимости с построенной теоретически, определяют как знак параметра ξ, так и его величину.