Компьютеризованный способ для оптимизированного по затратам расчета аэродинамических сил на летательном аппарате

Компьютеризованный способ для оптимизированного по затратам расчета аэродинамических сил на летательном аппарате

Иллюстрации

Показать все

Реферат

ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ

Настоящее изобретение относится к способам для содействия в конструировании летательных аппаратов созданием оптимизированных по затратам расчетов аэродинамических сил, испытываемых целым летательным аппаратом или компонентом летательного аппарата.

УРОВЕНЬ ТЕХНИКИ ИЗОБРЕТЕНИЯ

Общая ситуация в практических промышленных применениях, имеющих отношение к разработке изделий, состоит в необходимости выполнять многочисленные исследования внутри пространства параметров состояния. В конкретном случае авиации расчет аэродинамических сил, испытываемых компонентами летательного аппарата, является важным признаком, для того чтобы оптимально проектировать его конструктивные элементы, так чтобы вес конструкции был минимально возможным, но одновременно он был способен выдерживать ожидаемые аэродинамические силы.

Благодаря расширению использования возможности компьютерного моделирования текучих сред в наши дни определение аэродинамических сил на летательном аппарате обычно выполняется численным решением усредненных по Рейнолдсу уравнений Навье-Стокса (в дальнейшем, уравнений RANS), которые моделируют движение потока вокруг летательного аппарата, с использованием дискретных конечных элементов или моделей конечного объема. Из-за требований точности, поставленных в авиационной промышленности, каждое из этих вычислений требует существенных вычислительных ресурсов.

Определяющие размеры аэродинамические силы не известны априори, и, поскольку общая величина сил может зависеть от многих разных параметров полета, подобных углу атаки, углу бокового скольжения, числу Маха, углу отклонения поверхности управления, было необходимо выполнять много громоздких и дорогостоящих вычислений для надлежащего расчета максимальных аэродинамических сил, испытываемых разными компонентами летательного аппарата или летательным аппаратом в целом.

Для того чтобы сократить общее количество этих громоздких вычислений, в прошлом были разработаны технологии приближенного математического моделирования для получения модели пониженного порядка (ROM), подобные сингулярному разложению (SVD) в качестве средства для выполнения интеллектуальной интерполяции, или более точному собственно ортогональному разложению (в дальнейшем, POD), которое учитывает физику вопроса, используя проекцию Галеркина уравнений Навье-Стокса.

Идея этих технологий состоит в том, чтобы определять новое аналитическое решение в качестве комбинации информации, полученной раньше. POD определяет несколько мод, которые включают в себя решение, полученное вычислительной гидрогазодинамикой (CFD), а затем использует такие моды для воспроизводства решений, не полученных посредством CFD. Применение этих технологий может требовать многочисленных расчетов CFD, влекущих за собой большие вычислительные затраты.

Настоящее изобретение предназначено для решения этого недостатка.

СУЩНОСТЬ ИЗОБРЕТЕНИЯ

Цель настоящего изобретения состоит в том, чтобы предложить способы для производства аналитических расчетов аэродинамических сил, испытываемых летательным аппаратом в целом или компонентом летательного аппарата, которые зависимы от значительного количества параметров, с минимизацией вычислительных затрат.

Еще одна цель настоящего изобретения состоит в том, чтобы предложить способы для производства аналитических расчетов аэродинамических сил, испытываемых летательным аппаратом в целом или компонентом летательного аппарата, которые зависимы от значительного количества параметров, с минимизацией количества вычислений CFD.

Эти и другие цели удовлетворяются компьютеризованным способом, пригодным для содействия в конструировании летательного аппарата посредством предоставления значений одной или более размерных переменных, таких как распределение давления по поверхности крыла, для летательного аппарата в целом или компонента летательного аппарата, упомянутые одна или более переменных являются зависимыми от предопределенного набора параметров, такого как набор, включающий в себя угол атаки и число Маха, содержащим следующие этапы:

- Определение координатной сетки параметрического пространства, устанавливающей предопределенные расстояния между его значениями.

- Получение пригодной модели для расчета упомянутой одной или более размерных переменных для какой-нибудь точки в параметрическом пространстве посредством итерационного процесса по отношению к сокращенной группе точек, по увеличивающемуся количеству членов в каждой итерации, содержащей следующие подэтапы:

• Расчет значений упомянутых одной или более размерных переменных для начальной группы точек с использованием модели CFD.

• Получение начальной модели ROM из упомянутых вычислений CFD и расчет значений упомянутых одной или более размерных переменных для упомянутой начальной группы точек с использованием начальной модели ROM.

• Выбор точки e группы с наибольшим отклонением ε между результатами, выданными моделями CFD и ROM, и завершение итерационного процесса, если ε является меньшим, чем предопределенное значение ε₀.

• Выбор новых точек в параметрическом пространстве, которые должны быть добавлены в группу точек, в качестве точек, расположенных внутри координатной сетки параметрического пространства на предопределенном расстоянии от упомянутой точки e.

• Расчет значений упомянутых одной или более размерных переменных для новых точек с использованием модели CFD и ROM, и возврат на третий подэтап.

В частности, упомянутая одна или более размерных переменных включают в себя одно или более из следующего: аэродинамические силы, значения обшивки и распределение значений по летательному аппарату в целом или компоненту летательного аппарата; упомянутые параметры набора включают в себя одно или более из следующего: угол атаки и число Маха; а упомянутый компонент летательного аппарата является одним из следующих: крыло, горизонтальный стабилизатор, вертикальный стабилизатор.

В предпочтительном варианте осуществления упомянутый летательный аппарат в целом или компонент летательного аппарата поделен на блоки, а упомянутые модели CFD и ROM применяют блок за блоком. Таким образом, достигается точный способ для предоставления значений одной или более размерных переменных летательного аппарата или компонента летательного аппарата.

В еще одном предпочтительном варианте осуществления упомянутая модель ROM является моделью POD. CFD используется для расчета распределений давления для надлежащим образом выбранного набора точек в параметрическом пространстве, которые используются для аппроксимации, посредством POD и ad hoc интерполяции, размерных переменных в любой другой точке в параметрическом пространстве. В дополнение, способ минимизирует требуемое количество расчетов CFD (для минимизации вычислительных затрат, которые сильно зависят от этого количества) для заданного уровня погрешности. Это делается с использованием POD и интерполяции на уже рассчитанных точках. Новые точки выбираются итерационно, одна за другой или группами. Таким образом, достигается способ для предоставления значений одной или более размерных переменных летательного аппарата или компонента летательного аппарата, зависимых от предопределенного набора параметров, оптимизирующих вычислительные затраты.

Другие характеристики и преимущества настоящего изобретения будут ясны из последующего подробного описания вариантов осуществления, иллюстрирующих его цель, относительно приложенных фигур.

ОПИСАНИЕ ЧЕРТЕЖЕЙ

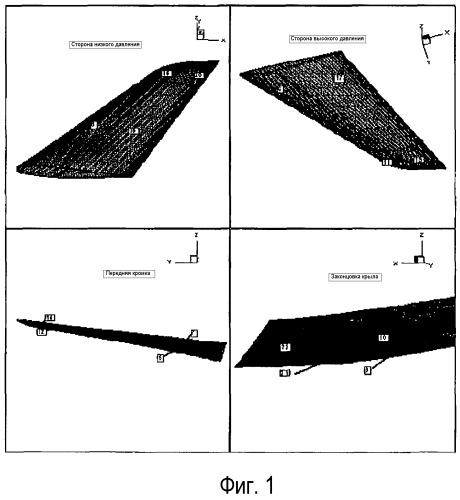
Фиг. 1 показывает виды стороны низкого давления, стороны высокого давления, передней кромки и законцовки крыла летательного аппарата, поделенных на блоки.

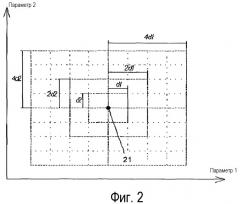
Фиг. 2 показывает графическое представление локальной координатной подсетки в координатной сетке параметрического пространства для выбора новых точек, которые должны добавляться в группу точек, используемых для получения модели POD согласно этому изобретению.

ПОДРОБНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ

Далее будет описан вариант осуществления способа согласно настоящему изобретению для получения модели POD, которая предоставляет возможность расчета распределения установившегося давления по поверхности крыла летательного аппарата, упомянутое распределение давления является зависимым от двух свободных параметров: угла атаки (α) и числа Маха (M).

Инициирующие этапы:

Этап 1: Деление крыла на несколько блоков согласно геометрии объекта. Инструментальные средства CFD обычно делят трехмерную вычислительную область на блоки, как проиллюстрировано на фиг. 1, показывающей крыло, поделенное на 16 основных блоков. Это является традиционной, но не существенной частью способа, который может применяться только с одним блоком.

Этап 2: Определение координатной сетки параметрического пространства выполняется установкой начального значения минимального расстояния по каждому параметру в параметрическом пространстве, d _l, l=1, ..., параметр #, которое получается из первого предположения наименьшего расстояния между точками в параметрическом пространстве на последующих этапах и могло бы нуждаться в некоторой калибровке. Такое расстояние будет уменьшено способом во время итерации, если необходимо. Затем координатная сетка с равными расстояниями определяется в параметрическом пространстве на основании этих расстояний. Такая координатная сетка будет развиваться во время процесса и может стать с неравными расстояниями.

Например, если угол атаки (α) в диапазоне от -3° до +3° и число Маха (M) в диапазоне от 0,40 до 0,80 являются рассматриваемыми параметрами, координатная сетка параметрического пространства может быть определена с установкой расстояний d_α=0,5 и d_M=0,05.

Этап 3: Запуск процесса для начальной группы точек в параметрическом пространстве, выбранных пользователем, таких как следующие

Начальная группа	Число Маха	Альфа
P1	0,400	-3,00
P2	0,600	-3,00
P3	0,800	-3,00
P4	0,400	0,00
P5	0,600	0,00
P6	0,800	0,00
P7	0,400	3,00
P8	0,600	3,00
P9	0,800	3,00

Введение новой группы точек

Этап 4: Применение, блок за блоком, POD к начальной группе точек. Зависящий от блока набор мод получают для каждого блока:

где P - распределение давления, x _i - пространственные координаты, α - угол атаки, M - число Маха, A _p - амплитуды мод, а столбцами матрицы φ i p являются моды POD. Каждая мода имеет ассоциативно связанное сингулярное значение, которое является следствием применения POD.

Этап 5: Классификация мод:

- Первая классификация (в каждом блоке) мод на две части является следующей: (a) те моды, которые дают RMSE, меньшее, чем некоторое пороговое значение ε_l (в зависимости от ε₀, после некоторой калибровки), игнорируются; (b) удерживаемые n₁ моды называются основными модами.

- Основные моды, в свою очередь, классифицируются на две группы, а именно n первичных мод и n₁ - n вторичных мод, причем с n, полученным после некоторой калибровки, скажем n = 4 5 n 1 .

Среднеквадратическая ошибка (RMSE) определяется в качестве

где N _p - общее количество точек сетки, которая определяет крыло, а error_i - разность между давлением по аппроксимации и давлением по решению CFD в i-й точке сетки.

Этап 6: Реконструкция POD распределения давления для каждой уже вычисленной группы точек с использованием (n) основных первичных мод в каждом блоке. Затем каждая точка дополнительно аппроксимируется с использованием соседних точек посредством метода наименьших квадратов.

Этап 7: Сравнение между рассчитанными посредством CFD и аппроксимированными посредством POD+интерполяция профилями давления и оценка RMSE в каждом блоке для каждых уже вычисленных точек.

RMSE для вышеупомянутой начальной группы из девяти точек, является следующим:

	RMSE
P1	0,0371
P2	0,0298
P3	0,0887
P4	0,0273
P5	0,0190
P6	0,0756
P7	0,0605
P8	0,0930
P9	0,1758

Этап 8: Выбор точки с наибольшим RMSE.

Как показано в вышеприведенной таблице, в первой итерации этой точкой является P9.

Этап 9: Определение, как показано на фиг. 2, локальной координатной подсетки из общей координатной сетки параметрического пространства поблизости от точки 21 максимальной ошибки. Такая локальная координатная подсетка состоит из трех уровней, на расстояниях d_l (первый уровень), 2d_l (второй уровень) и 4d_l (третий уровень).

Этап 10: Выбор уровня, на котором будет введена новая точка. Если есть некоторые точки между двумя уровнями (смотрите ниже), они считаются принадлежащими внутреннему уровню.

• Если никаких точек не присутствует во всей координатной подсетке, то новая точка вводится на третьем уровне.

• Если только третий уровень демонстрирует точки, то новая точка вводится на втором уровне.

• Если на первом уровне нет точек и есть только одна точка на втором уровне, новая точка вводится на втором уровне.

• Если на первом уровне нет точек и есть по меньшей мере две точки на втором уровне, новая точка вводится на первом уровне.

• Если по меньшей мере одна точка присутствует на первом уровне, то новая точка вводится на первом уровне с одним исключением, которое приводит к введению подуровня в локальной координатной сетке. Это происходит, когда (a) по меньшей мере пять точек присутствуют на первом уровне и (b) по меньшей мере четыре из них показывают наибольшее RMSE среди всех точек на трех уровнях. В таком случае, расстояния в локальной координатной подсетке делятся на два, а этап 9 повторяется вновь с получающейся в результате новой координатной подсеткой. Отметим, что этот этап подразумевает, что каждая точка обычно будет иметь разный набор минимальных расстояний d _l.

В рассматриваемом примере, новая точка P10 будет введена на третьем уровне, так как ни одна из точек начальной группы не присутствует во всей координатной подсетке поблизости от P9.

Этап 11:

Как только был выбран заданный уровень, точка наибольшего заполнения пространства на этом уровне выбирается как изложено ниже.

Вычисляется минимальное расстояние D от каждого возможного кандидата до остальных, уже выбранных точек. Выбирается тот кандидат, который показывает наибольшее значение D. D - расстояние в параметрическом пространстве. В этом примере расстояние между двумя точками параметрического расстояния (помеченными 1 и 2) определяется, как изложено ниже:

,

где α 12 = α 2 − α 1 Δ α и M 12 = M 2 − M 1 Δ M - расстояния в параметрах α и M, а Δα и ΔM - соответствующие полные диапазоны в этих параметрах.

В рассматриваемом примере, расстояние между точками третьего уровня и ближайшей точкой, принадлежащей группе, показано в следующей таблице.

Точки третьего уровня	Ближайшая точка группы	Расстояние
Mach	Alpha	Mach	Alpha
0,650	3,00	0,600	3,00	0,1250
0,650	2,50	0,600	3,00	0,1502
0,650	2,00	0,600	3,00	0,2083
0,650	1,50	0,600	0,0	0,2795
0,700	1,50	0,600	0,0	0,3536
0,750	1,50	0,800	0,0	0,2795
0,800	1,50	0,800	0,0	0,2500

Поэтому новой точкой, которая должна быть введена, является P10: Число Маха=0,700, альфа=1,50.

Этап 12: Если более чем одна точка введена на каждой итерации, то процесс повторяется от этапа 8 с исключенными уже выбранными точками.

Обновление набора мод:

Как только новая точка (или группа точек) была вычислена, набор мод для каждого блока обновляется.

Этап 13: Применение POD к группе точек, игнорируя те моды, которые показывают RMSE, меньшую, чем ε₁.

Этап 14: Вычисление некоторых псевдоточек, определяемых блок за блоком, которые состоят из двух групп:

• n₁ основных мод каждого блока, умноженных на свои соответственные сингулярные значения,

• Моды POD, полученные при применении POD к новым точкам, являющимся результатом из последней итерации, умноженным на свои соответственные сингулярные значения.

Этапы 13 и 14 могут быть свернуты во всего лишь только один этап. В этом случае, псевдоточки определяются сложением основных мод уже вычисленных точек, умноженных на их соответственные сингулярные значения, и новых точек. Деление на этапы 13 и 14, как приведено выше, сделано для отфильтровывания численных ошибок из процесса, что является широко известным преимуществом способа с POD.

Этап 15: Применение POD к набору всех псевдоточек, блок за блоком.

Этап 16: Повторение процесса, начиная с этапа 5.

Для иллюстрации этого итерационного процесса следует краткое описание второй итерации в рассматриваемом примере:

RMSE для группы из десяти точек на второй итерации является следующей:

	RMSE
P1	0,0313
P2	0,0242
P3	0,0723
P4	0,0275
P5	0,0167
P6	0,0569
P7	0,0853
P8	0,0458
P9	0,1421
P10	0,0260

Точкой максимальной ошибки EI по-прежнему является P9, и новая точка P11 будет введена на втором уровне, так как нет ни одной точки в группе на уровнях 1 и 2, и есть точка на уровне 3 (P10, введенная на первой итерации).

Расстояние между точками второго уровня и ближайшей точкой, принадлежащей группе, показано в следующей таблице:

Точки второго уровня	Ближайшая точка группы	Расстояние
Mach	Alpha	Mach	Alpha
0,700	3,00	0,800	3,00	0,2500
0,700	2,50	0,700	1,50	0,1667
0,700	2,00	0,700	1,50	0,0833
0,750	2,00	0,700	1,50	0,1502
0,750	2,00	0,800	3,00	0,1662

Поэтому новой точкой, которая должна быть введена, является P11: Число Маха=0,700, альфа=2,50.

Критерии останова:

Этап 17: Процесс завершается, когда RMSE, вычисленная на этапе 7 с использованием POD, и обе, линейная и квадратичная интерполяция методом наименьших квадратов, являются меньшими, чем ε₀ .

Результаты

При выполнении способа в рассматриваемом примере начальная группа точек в параметрическом пространстве, как упомянуто раньше, была следующей:

	Число Маха	Альфа
P1	0,400	-3,00
P2	0,600	-3,00
P3	0,800	-3,00
P4	0,400	0,00
P5	0,600	0,00
P6	0,800	0,00
P7	0,400	3,00
P8	0,600	3,00
P9	0,800	3,00

Во время итерационного процесса следующие точки были добавлены в группу:

P10	0,700	1,50
P11	0,700	2,50
P12	0,800	2,00
P13	0,500	1,50
P14	0,750	2,50
P15	0,400	2,00
P16	0,700	-1,00
P17	0,750	1,50
P18	0,750	3,00
P19	0,800	-1,50

P20	0,500	2,50
P21	0,800	2,50
P22	0,800	1,50
P23	0,700	0,50
P24	0,750	1,00
P25	0,700	3,00
P26	0,750	2,00
P27	0,450	2,50
P28	0,800	1,00
P29	0,450	3,00
P30	0,750	-0,50

Оценка модели, полученной согласно способу по этому изобретению, может быть выполнена, сравнивая результаты, полученные в 16 контрольных точках с использованием упомянутой модели на нескольких итерациях, с результатами, полученными с использованием модели CFD, которые показаны в следующих таблицах:

Коэффициент подъемной силы	CFD	Результаты модели по изобретению
Конт-роль-ная точка	Число Маха	Альфа	10 точек	15 точек	20 точек	25 точек	30 точек
Tp1	0,800	2,25	0,1965	0,1922	0,1966	0,1965	0,1971	0,1966
Tp2	0,800	1,25	0,1045	0,1061	0,1082	0,1075	0,1054	0,1058
Tp3	0,800	-1,25	-0,1077	-0,1089	-0,1085	-0,1073	-0,1082	-0,1088
Tp4	0,800	-2,25	-0,1920	-0,1871	-0,1925	-0,1927	-0,1928	-0,1936
Tp5	0,775	2,25	0,1895	0,1899	0,1899	0,1903	0,1910	0,1900
Tp6	0,775	1,25	0,1012	0,1036	0,1051	0,1031	0,1023	0,1018
Tp7	0,775	-1,25	-0,1048	-0,1018	-0,1121	-0,1057	-0,1066	-0,1068
Tp8	0,775	-2,25	-0,1867	-0,1853	-0,1884	-0,1908	-0,1912	-0,1916
Tp9	0,725	2,25	0,1773	0,1849	0,1778	0,1788	0,1777	0,1774
Tp10	0,725	1,25	0,0966	0,0971	0,0980	0,0965	0,0970	0,0970
Tp11	0,725	-1,25	-0,1002	-0,0962	-0,1078	-0,1022	-0,1029	-0,1022
Tp12	0,725	-2,25	-0,1785	-0,1812	-0,1816	-0,1829	-0,1867	-0,1864
Tp13	0,525	2,25	0,1577	0,1565	0,1267	0,1563	0,1561	0,1585
Tp14	0,525	1,25	0,0868	0,0722	0,0845	0,0847	0,0873	0,0854
Tp15	0,525	-1,25	-0,0897	-0,0749	-0,0960	-0,0786	-0,0964	-0,1084
Tp16	0,525	-2,25	-0,1600	-0,1580	-0,1598	-0,1196	-0,1199	-0,1197

Коэффициент механическогомомента X	CFD	Результаты модели по изобретению
Конт-рольная точка	Число Маха	Альфа	10 точек	15 точек	20 точек	25 точек	30 точек
Tp1	0,800	2,25	+0,2062	0,1979	0,2054	0,2054	0,2068	0,2061
Tp2	0,800	1,25	+0,1109	0,1124	0,1181	0,1174	0,1128	0,1127
Tp3	0,800	-1,25	-0,1018	-0,1023	-0,1024	-0,1010	-0,1016	-0,1022
Tp4	0,800	-2,25	-0,1866	-0,1810	-0,1867	-0,1866	-0,1866	-0,1870
Tp5	0,775	2,25	+0,1991	0,1957	0,1984	0,1992	0,2010	0,1995
Tp6	0,775	1,25	+0,1078	0,1102	0,1140	0,1117	0,1090	0,1085
Tp7	0,775	-1,25	-0,0987	-0,0953	-0,1067	-0,0993	-0,0999	-0,1000
Tp8	0,775	-2,25	-0,1812	-0,1790	-0,1824	-0,1846	-0,1848	-0,1850
Tp9	0,725	2,25	+0,1849	0,1910	0,1858	0,1875	0,1853	0,1849
Tp10	0,725	1,25	+0,1036	0,1041	0,1060	0,1029	0,1036	0,1037
Tp11	0,725	-1,25	-0,0939	-0,0894	-0,1018	-0,0955	-0,0959	-0,0954
Tp12	0,725	-2,25	-0,1728	-0,1746	-0,1749	-0,1760	-0,1798	-0,1796
Tp13	0,525	2,25	+0,1654	0,1644	0,1279	0,1637	0,1637	0,1658
Tp14	0,525	1,25	+0,0943	0,0809	0,0926	0,0928	0,0953	0,0933
Tp15	0,525	-1,25	-0,0827	-0,0668	-0,0879	-0,0704	-0,0879	-0,1001
Tp16	0,525	-2,25	-0,1534	-0,1499	-0,1514	-0,1100	-0,1100	-0,1096

Коэффициент механического момента Y	CFD	Результаты модели по изобретению
Контрольная точка	Число Маха	Альфа	10 точек	15 точек	20 точек	25 точек	30 точек
Tp1	0,800	2,25	-0,1068	-0,1044	-0,1076	-0,1074	-0,1081	-0,1076
Tp2	0,800	1,25	-0,0345	-0,0377	-0,0392	-0,0387	-0,0361	-0,0363
Tp3	0,800	-1,25	+0,1270	0,1278	0,1279	0,1266	0,1273	0,1278
Tp4	0,800	-2,25	+0,1914	0,1877	0,1921	0,1921	0,1923	0,1928
Tp5	0,775	2,25	-0,1036	-0,1036	-0,1038	-0,1044	-0,1054	-0,1043
Tp6	0,775	1,25	-0,0340	-0,0374	-0,0384	-0,0367	-0,0351	-0,0347
Tp7	0,775	-1,25	+0,1232	0,1215	0,1295	0,1241	0,1247	0,1248
Tp8	0,775	-2,25	+0,1858	0,1853	0,1878	0,1892	0,1896	0,1898
Tp9	0,725	2,25	-0,0960	-0,1017	-0,0970	-0,0982	-0,0967	-0,0965
Tp10	0,725	1,25	-0,0335	-0,0344	-0,0356	-0,0337	-0,0338	-0,0338
Tp11	0,725	-1,25	+0,1171	0,1151	0,1241	0,1188	0,1193	0,1188
Tp12	0,725	-2,25	+0,1770	0,1800	0,1805	0,1807	0,1833	0,1831
Tp13	0,525	2,25	-0,0868	-0,0877	-0,0618	-0,0849	-0,0847	-0,0867
Tp14	0,525	1,25	-0,0321	-0,0233	-0,0302	-0,0302	-0,0321	-0,0307
Tp15	0,525	-1,25	+0,1029	0,0911	0,1067	0,0924	0,1078	0,1172
Tp16	0,525	-2,25	+0,1564	0,1542	0,1548	0,1219	0,1221	0,1218

Модификации могут быть внесены в предпочтительный, только что изложенный вариант осуществления, которые содержатся в пределах объема, определенного следующей формулой изобретения.

1. Компьютеризованный способ, пригодный для содействия в конструировании летательного аппарата посредством предоставления значений одной или более размерных переменных для летательного аппарата в целом или компонента летательного аппарата, упомянутые одна или более переменных являются зависимыми от предопределенного набора параметров, отличающийся тем, что содержит следующие этапы, на которых:a) определяют координатную сетку параметрического пространства, устанавливающую предопределенные расстояния между его значениями;b) получают пригодную модель для расчета упомянутых одной или более размерных переменных для какой-нибудь точки в параметрическом пространстве посредством итерационного процесса по отношению к сокращенной группе точек, по увеличивающемуся количеству членов в каждой итерации, содержащему следующие подэтапы, на которых:b1) рассчитывают значения упомянутых одной или более размерных переменных для начальной группы точек с использованием модели CFD;b2) получают начальную модель ROM из упомянутых вычислений CFD и рассчитывают значения упомянутых одной или более размерных переменных для упомянутой начальной группы точек с использованием начальной модели ROM;b3) выбирают точку ε группы с наибольшим отклонением ε между результатами, выданными моделями CFD и ROM, и завершают итерационный процесс, если ε является меньшим, чем предопределенное значение ε₀;b4) выбирают новые точки в параметрическом пространстве, которые должны быть добавлены в группу точек, в качестве точек, расположенных внутри координатной сетки параметрического пространства на предопределенном расстоянии от упомянутой точки e;b5) рассчитывают значения упомянутых одной или более размерных переменных для новых точек с использованием модели CFD и ROM и возвращаются на подэтап b3).

2. Компьютеризованный способ по п.1, отличающийся тем, что упомянутый летательный аппарат в целом или компонент летательного аппарата поделен на блоки, а упомянутые модели CFD и ROM применяются блок за блоком.

3. Компьютеризованный способ по любому из пп.1-2, отличающийся тем, что упомянутая одна или более размерных переменных включают в себя одно или более из следующего: аэродинамические силы, значения обшивки, распределение значений по летательному аппарату в целом или компоненту летательного аппарата.

4. Компьютеризованный способ по любому из пп.1-2, отличающийся тем, что упомянутые параметры набора включают в себя одно или более из следующего: угол атаки, число Маха.

5. Компьютеризованный способ по любому из пп.1-2, отличающийся тем, что упомянутый компонент летательного аппарата является одним из следующего: крыло, горизонтальный стабилизатор, вертикальный стабилизатор.

6. Компьютеризованный способ по любому из пп.1-2, отличающийся тем, что упомянутая модель ROM является моделью POD.

7. Компьютеризованный способ по п.6, отличающийся тем, что отклонение ε между результатами, выданными моделями CFD и POD, получают в качестве среднеквадратической ошибки между упомянутыми результатами.

8. Компьютеризованный способ по п.6, отличающийся тем, что модель POD получают исключением наименее значимых мод из группы точек.

9. Компьютеризованный способ по п.7, отличающийся тем, что модель POD получают исключением наименее значимых мод из группы точек.