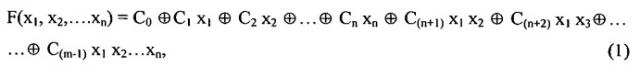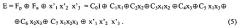Способ реализации логических преобразователей
Иллюстрации
Показать всеИзобретение относится к цифровой вычислительной технике. Техническим результатом является создание библиотечных модулей полиномиальных логических преобразователей на языках HDL, а также оперативной перенастройки логических преобразователей на реализацию заданной логической функции. Технический результат достигается за счет способа, который включает первоначальное получение исходного математического описания рабочего закона функционирования n-входовых логических преобразователей в виде полинома Жегалкина общего вида, затем разработку и реализацию схемы формирователя всех 2n монотонных конъюнкций полинома Жегалкина, затем разработку и реализацию двух последовательных цепочек, каждая из которых содержит по (2n-1) двухвходовых элементов неравнозначности. 7 ил.
Реферат
Изобретение относится к области автоматики и цифровой вычислительной техники и может быть использовано для создания сложных n-входовых логических преобразователей (комбинационных автоматов) с самопроверкой правильности функционирования в рабочем режиме и оперативной перенастройкой на реализацию любой логической функции, зависящей от n аргументов.
Известен способ и вариант его технической реализации [1], который включает первоначальное получение исходного математического описания рабочего закона функционирования n-входовых логических преобразователей в тестопригодном логическом базисе Жегалкина, затем разработку и реализацию структурной схемы логического преобразователя из элемента генератор логической 1, r последовательных цепочек из (k-1) двухвходовых логических элементов с электронно перестраиваемой логической функцией, реализующих k-аргументные функции «И» в рабочем режиме или функции равнозначности в режиме тестирования, и последовательной цепочки из (r-1) двухвходовых элементов неравнозначности, реализующих рабочую функцию Fр путем свертки по модулю два всех k-аргументных конъюнкций, определение в последующем n тестовых M-последовательностей из одного и того же замкнутого класса и эталонной M-последовательности, которую алгоритмически формируют из n тестовых M-последовательностей, причем в режиме тестирования тестовые и эталонную M-последовательности одновременно генерируют внешним n-разрядным регистром сдвига с линейной обратной связью на предельно возможной рабочей частоте логического преобразователя.
Данный способ обеспечивает высокую тестопригодность логических преобразователей как для их статического, так и динамического тестирования на предельной рабочей частоте путем электронного переключения из рабочего режима в режим тестирования M-последовательностями. Однако данный способ не обеспечивает максимальной надежности функционирования логических преобразователей непосредственно в рабочем режиме.
Наиболее близким по технической сути является способ реализации логических преобразователей [2], состоящий в том, что он включает первоначальное получение исходного математического описания рабочего закона функционирования n-входовых логических преобразователей в виде полинома Жегалкина общего вида, затем разработку и реализацию схемы формирователя всех 2n монотонных конъюнкций полинома Жегалкина из элемента генератор логической 1, входных переменных и последовательных цепочек из двухвходовых логических элементов с электронно перестраиваемой логической функцией, которые в рабочем режиме логического преобразователя реализуют k-аргументные функции «И», а в режиме тестирования функции равнозначности, затем разработку и реализацию первой последовательной цепочки из (r-1) двухвходовых элементов неравнозначности, которые реализует рабочую функцию Fр путем свертки по модулю два r конъюнкций, поступающих с формирователя конъюнкций и входящих в найденный полином Жегалкина с коэффициентом единица, и второй последовательной цепочки из (s-1) элементов неравнозначности для формирования вспомогательной функции Fв путем свертки по модулю два s конъюнкций, поступающих с формирователя конъюнкций и входящих в найденный полином Жегалкина с коэффициентом ноль, причем s+r=2n, после чего осуществляют формирование признака ошибки путем суммирования по модулю два рабочей функции Fр, вспомогательной функции Fв и дополнительной n-аргументной конъюнкции инверсных значений всех входных переменных.
Данный способ реализации повышает надежность функционирования логических преобразователей путем придания им дополнительного свойства самопроверяемости в режиме работы. Однако, для этого требуется разработка и реализация индивидуальной схемы коммутации для подклчения соответствующих конъюнкций к каждой из двух последовательных цепочек из элементов неравнозначности, причем количество элементов в каждой из этих цепочек являются переменными величинами, зависящими от реализуемой логической функции. Данное обстоятельство не позволяет создавать библиотечные модули полиномиальных логических преобразователей на языках HDL, а также оперативно перенастраивать логические преобразователи на реализацию заданной логической функции.
Изобретение направлено на усовершенствование способа реализации n-входовых логических преобразователей, что позволит создавать библиотечные модули полиномиальных логических преобразователей на языках HDL, а также оперативную перенастройку логических преобразователей на реализацию заданной логической функции.
Это достигается тем, что первую и вторую последовательные цепочки из элементов равнозначности впоследствии дополняют до (2n-1) элементов неравнозначности, при этом одна цепочка реализует рабочую функцию Fр, а другая реализует вспомогательную функцию Fв путем свертки по модулю два любых сочетаний r и s конъюнкций соответственно, которые перераспределяют между первой и второй последовательными цепочками из двухвходовых элементов неравнозначности электронным коммутатором на основе 2n-разрядного последовательного регистра сдвига, для чего в него по окончании реализации с помощью внешних средств вводят изначально найденный полином Жегалкина общего вида в виде двоичного вектора всех 2n коэффициентов значений конъюнкций полинома, при этом неиспользуемые s конъюнкций в первой цепочке и r конъюнкций во второй цепочке оказываются приравненными нулю.
Для осуществления предлагаемого изобретения закон функционирования n-входового логического преобразователя исходно должен быть задан полиномом Жегалкина, общий вид которого может быть представлен следующим образом:
где xi - i-я входная логическая переменная;
Cj - j-й коэффициент, указывающий на необходимость реализации соответствующей конъюнкции при Cj=1;
xixf…xg - некоторая k-аргументная конъюнкция логических переменных;
m=2n; Cj={0,1}, j=0,(2n-1); xi={0,1}, i=1,n.
Сочетание переменных в правой части (1), например, C(m-1)x1x2…xn, следует понимать как их логическое произведение (конъюнкцию), т.е.
C(m-1)x1x2…xn=C(m-1)&x1&x2&…&xn
Запишем выражение (1) несколько иначе:
где конъюнкция К0=1 представляет единичную конъюнкцию, которая реализуется генератором логической 1.
Широко известно, что в выражении (2) все коэффициенты Cj будут равны 1 только в том случае, если реализуется логическая функция n-аргументной конъюнкции инверсий входных аргументов, то есть
где следует понимать как инверсию xi.
Тогда, в соответствии с законами алгебры логики относительно операции неравнозначности, можно выражение (3) преобразовать к виду
В зависимости от того, какую именно логическую функцию должен реализовывать n-входовый логический преобразователь, предварительно определяют значения соответствующих коэффициентов Cj для логической функции (Fр), реализуемой в рабочем режиме, что может быть осуществлено широко известным методом неопределенных коэффициентов [3]. Тогда, как следует из выражения (4), если r конъюнкций, обеспечивающих реализацию рабочей функции Fр, оставить в левой части выражения (4), а оставшиеся (s+1) конъюнкций перенести в правую часть этого выражения, то они будут равны при любых значениях входных аргументов. Это обеспечивает в прототипе самопроверяемость логических преобразователей в рабочем режиме функционирования путем использования двух последовательных цепочек из (r-1) и (s-1) двухвходовых элементов неравнозначности, которые формируют на выходе признак ошибки путем реализации свертки по модулю два значения функции Fр с выхода последовательной цепочки из (r-1) элементов неравнозначности, значения вспомогательной функции Fв с выхода последовательной цепочки из (s-1) элементов неравнозначности и дополнительной n-аргументной конъюнкции инверсий входных аргументов, причем сумма s+r=2n. Как видно, по способу-прототипу требуется разработка и реализация индивидуальной схемы коммутации для подключения соответствующих конъюнкций к каждой из двух последовательных цепочек из элементов неравнозначности, причем количество элементов в каждой из этих цепочек являются переменными величинами, зависящими от реализуемой логической функции.
Рассмотрим осуществление заявляемого способа реализации логического преобразователя, количество входных переменных которого равно трем.
Обобщенное математическое описание самопроверяемых 3-входовых логических преобразователей в виде полинома Жегалкина общего вида представимо следующим образом:
Значениями коэффициентов Ci задается реализуемая логическая функция. Например, если уравнение (5) имеет вид
то
и
Соотношениям (7) и (8) соответственно эквивалентны соотношения (9) и (10):
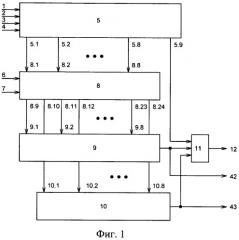
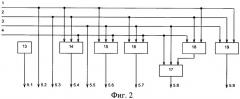
На фиг. 1 представлена структурная схема самопроверяемого логического преобразователя, соответствующая заявляемому изобретению и разработанная на основе соотношений (6), (9) и (10); на фиг. 2 - структурная схема формирователя конъюнкций 5; на фиг. 3 - структурная схема электронного коммутатора конъюнкций 8; на фиг. 4 - структурная схема X логического элемента VAR с электронно перестраиваемой логической функцией; на фиг. 5 - структурная схема Y одной секции электронного коммутатора конъюнкций 8; на фиг. 6 - структурная схема первой последовательной цепочки 9 из элементов неравнозначности; на фиг. 7 - структурная схема второй 10 последовательной цепочки из элементов неравнозначности.
Входные логические переменные x1, x2, x3 подаются соответственно на входы 1, 2, 3 формирователя конъюнкций 5. Формирователь конъюнкций 5 содержит генератор логической единицы 13, элементы VAR 14, 15, 16, 17, 18 и элемент 19, реализующий логическую функцию . На вход 4 формирователя конъюнкций 5 подается сигнал управления u, переводящий логический преобразователь в режим работы (u=1) или в режим тестирования (u=0). Вход 1 формирователя конъюнкций 5 подключен к выходу 5.2, входам 14.3, 15.3 и 18.3 элементов VAR 14, 15, 18 и первому входу элемента 19. Вход 2 формирователя конъюнкций 5 подключен к выходу 5.3, к входам 14.4, 16.4, 18.4 элементов VAR 14, 16, 18 и второму входу элемента 19. Вход 3 формирователя конъюнкций 5 подключен к выходу 5.5, к входам 15.4, 16.3, 17.3 элементов VAR 15,16,17 и третьему входу элемента 19. Выход 18.6 элемента VAR 18 подключен к входу 17.4 элемента VAR 17. Вход 4 формирователя конъюнкций 5 подключен к управляющим входам 14.5, 15.5, 16,5, 17.5, 18.5 элементов VAR 14, 15, 16, 17, 18. Выходы 14.6, 15.6, 16.6, 17.6 элементов VAR 14, 15, 16, 17 подключены соответственно к выходам 5.4, 5.6, 5.7, 5.8 формирователя конъюнкций 5, а его выходы 5.1 и 5.9 подключены соответственно к выходам генератора логической единицы 13 и элемента 19. В режиме работы (u=1) элементы VAR 14, 15, 16, 17, 18 реализуют двухаргументные функции «И», а последовательные их цепочки реализуют k-аргументные функции «И». Таким образом, на выходах 5.1, 5.2, 5.3, 5.4, 5.5, 5.6, 5.7, 5.8 формирователя конъюнкций 5 в рабочем режиме соответственно формируются все монотонные конъюнкции K0=1; K1=x1; K2=x2; K3=x1x2; K4=x3; K5=x1x3; K6=x2x3; K7=x1x2x3 логической функции трех аргументов x1, x2, x3. Выход 5.9 формирователя конъюнкций 5 подключен к выходу элемента 19, который подключен к первому входу сумматора по модулю два 11, второй вход которого соединен с выходом 42 первой цепочки из элементов неравнозначности 9, а третий вход элемента 11 соединен с выходом 43 второй цепочки из элементов неравнозначности 10. Выход 12 логического преобразователя, на котором формируется сигнал ошибки E, подключен к выходу элемента 11. Каждый из элементов VAR 14, 15, 16, 17, 18 реализует следующую логическую функцию
где a и b - некоторые переменные, поступающие соответственно на входы 14.3 и 14.4, 15.3 и 15.4, 16.3 и 16.4, 17.3 и 17.4, 18.3 и 18.4); u - сигнал управления, поступающий на входы 14.5, 15.5, 16.5, 17.5, 18.5. В каждом элементе VAR 14, 15, 16, 17, 18 вход X.3 (X=14, 15, 16, 17, 18) является первым входом элемента VAR, подключенным к первому входу элемента «И» X.1 и второму входу элемента «ИЛИ-НЕ» X.2, вход X.4 является вторым входом элемента VAR, подключенным к второму входу элемента X.1 и первому входу элемента X.2, третий вход которого подключен к третьему входу X.5 элемента VAR, выход элемента X.2 соединен с первым входом элемента «ИЛИ» X4, второй вход которого соединен с выходом элемента X.1, а выход элемента X.4 является выходом элемента VAR. Выходы 5.1, 5.2, 5.3, 5.4, 5.5, 5.6, 5.7, 5.8 формирователя конъюнкций 5 соответственно соединены с входами 8.1, 8.2, 8.3, 8.4, 8.5, 8.6, 8.7, 8.8 электронного коммутатора конъюнкций 8, состоящего из последовательно соединенных однотипных секций 20, 21, 22, 23, 24, 25, 26, 27, выполненных на основе синхронных D-триггеров и образующих в совокупности регистр сдвига. Каждая секция Y (Y=20, 21, 22, 23, 24, 25, 26, 27) содержит один синхронный D-триггер Y.1, единичный выход которого соединен с вторым входом первого элемента «И» Y.2 и выходом секции Y.6, а нулевой выход триггера соединен с первым входом второго элемента «И» Y.3, второй вход которого соединен с первым входом первого элемента «И» и соответствующим входом электронного коммутатора конъюнкций 8. Выход первого элемента «И» Y.2 и выход второго элемента «И» Y.3 подключены к соответствующим выходам электронного коммутатора конъюнкций 8. Выход Y.6 предшествующей секции соединен с входом Y.4 последующей секции. Выход 27.4 последней секции 27 ни к чему не подключается. Вход 20.4 первой секции 20 соединен с входом 6 электронного коммутатора конъюнкций 8, который предназначен для последовательного ввода в электронный коммутатор конъюнкций 8 с помощью внешних средств изначально найденного полинома Жегалкина общего вида в виде двоичного вектора всех 2n коэффициентов значений конъюнкций полинома, начиная со старшей (K7) конъюнкции. Входы Y.5 всех секций 20, 21, 22, 23, 24, 25, 26, 27 объединены между собой и подключены к входу 7 электронного коммутатора конъюнкций 8. На вход 7 подаются внешние тактовые импульсы, синхронизирующие ввод в электронный коммутатор конъюнкций 8 двоичного вектора всех 2n коэффициентов значений конъюнкций полинома. Выходы 8.9, 8.11, 8.13, 8.15, 8.17, 8.19, 8.21, 8.23 электронного коммутатора конъюнкций 8 соответственно соединены с входами 9.1, 9.2. 9.3, 9.4, 9.5, 9.6, 9.7, 9.8, которые являются входами первой цепочки 9 из последовательно соединенных сумматоров по модулю два 28, 29, 30, 31, 32, 33, 34. Выход 42 первой цепочки сумматоров 9 по модулю два соединен с вторым входом сумматора по модулю два 11 и с первым выходом логического преобразователя, где формируется вспомогательная логическая функция FB. Выходы 8.10, 8.12, 8.14, 8.16, 8.18, 8.20, 8.22, 8.24 электронного коммутатора конъюнкций 8 соответственно соединены с входами 10.1, 10.2. 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, которые являются входами второй цепочки 10 из последовательно соединенных сумматоров по модулю два 35, 36, 37, 38, 39, 40, 41. Выход 43 второй цепочки сумматоров по модулю два 10 соединен с третьим входом сумматора по модулю два 11 и с вторым выходом логического преобразователя, где формируется рабочая логическая функция Fр.
Логический преобразователь, реализованный по заявляемому способу, работает следующим образом: на вход 4 логического преобразователя подается сигнал, равный логической 1, то есть преобразователь переводится в рабочий режим. Далее с помощью внешних средств в электронный коммутатор конъюнкций 8 вводится изначально найденный полином Жегалкина общего вида в виде двоичного вектора всех 2n коэффициентов значений конъюнкций полинома. После этого триггеры электронного коммутатора конъюнкций 8 установятся в соответствующие состояния и осуществят перераспределение конъюнкций в соответствии с введенным двоичным вектором: r конъюнкций, поступающих с формирователя конъюнкций 5 и входящих в найденный полином Жегалкина с коэффициентом единица, будут направлены на соответствующие входы второй последовательной цепочки из сумматоров по модулю два 10, a s конъюнкций, поступающих с формирователя конъюнкций 5 и входящих в найденный полином Жегалкина с коэффициентом ноль, будут направлены на соответствующие входы первой последовательной цепочки из сумматоров по модулю два 9. При правильной работе логического преобразователя на его выходе 12 должен формироваться логический ноль при любых наборах входных переменных x1, x2, x3. Достоверное значение сигнала на выходе 12 логического преобразователя устанавливается с запаздыванием по отношению ко времени изменения значений входных сигналов, минимальная величина которого может быть определена как τ=mtзп, где m - количество последовательно включенных элементов неравнозначности, a tзп - время задержки их переключения. В связи с этим опрос сигналов на выходах 12, 42 и 43 логического преобразователя необходимо производить не ранее чем через τ после смены значений входных переменных x1, x2, x3.
Техническим результатом от использования заявляемого изобретения является усовершенствование способа реализации n-входовых логических преобразователей, позволяющее создавать библиотечные модули полиномиальных логических преобразователей на языках HDL, а также оперативную перенастройку логических преобразователей на реализацию заданной логической функции как на этапе проектирования, так и непосредственно в режиме работы логического преобразователя.
Источники информации
1. Патент RU 2413282 C2 Российская Федерация, МПК6 G06F 11/26. Способ тестопригодной реализации логических преобразователей / Акинина Ю.С.(RU), Подвальный С.Л. (RU), Тюрин C.B. (RU), заявитель и патентообладатель ГОУ ВПО «Воронежский госуд. техн. ун-т.(RU) - №2008151028/08; заявл. 22.12.2008; опубл. 27.02.2011, Бюл. №6.
2. Патент RU 2497182 C2 Российская Федерация, МПК6 G06F 11/00. Способ тестопригодности реализации логических преобразователей / Акинин A.A. (RU), Акинина Ю.С.(RU), Подвальный С.Л. (RU), Тюрин C.B. (RU), заявитель и патентообладатель ГОУ ВПО «Воронежский госуд. техн. ун-т.(RU) - №2011123026/08; заявл. 07.06.2011; опубл. 27.10.2013, Бюл. №30.
3. Гаврилов Г.П., Сапоженко A.A. Задачи и упражнения по дискретной математике. - М.: Физматлит, 2005. - 460 с.
Способ реализации логических преобразователей, включающий первоначальное получение исходного математического описания рабочего закона функционирования n-входовых логических преобразователей в виде полинома Жегалкина общего вида, затем разработку и реализацию схемы формирователя всех 2n монотонных конъюнкций полинома Жегалкина из элемента генератор логической 1, входных переменных и последовательных цепочек из двухвходовых логических элементов с электронно перестраиваемой логической функцией, которые в рабочем режиме логического преобразователя реализуют k-аргументные функции «И», а в режиме тестирования - функции равнозначности, затем разработку и реализацию первой последовательной цепочки из (r-1) двухвходовых элементов неравнозначности, которые реализует рабочую функцию Fр путем свертки по модулю два r конъюнкций, поступающих с формирователя конъюнкций и входящих в найденный полином Жегалкина с коэффициентом единица, и второй последовательной цепочки из элементов неравнозначности для формирования вспомогательной функции Fв путем свертки по модулю два s конъюнкций, поступающих с формирователя конъюнкций и входящих в найденный полином Жегалкина с коэффициентом ноль, причем s+r=2n, после чего осуществляют формирование признака ошибки путем суммирования по модулю два рабочей функции Fр, вспомогательной функции Fв и дополнительной n-аргументной конъюнкции инверсных значений всех входных переменных, отличающийся тем, что первую и вторую последовательные цепочки из элементов равнозначности впоследствии дополняют до (2n-1) элементов неравнозначности, при этом одна цепочка реализует рабочую функцию Fр, а другая реализует вспомогательную функцию Fв путем свертки по модулю два любых сочетаний r и s конъюнкций соответственно, которые перераспределяют между первой и второй последовательными цепочками из двухвходовых элементов неравнозначности электронным коммутатором на основе 2n-разрядного последовательного регистра сдвига, для чего в него по окончании реализации с помощью внешних средств вводят изначально найденный полином Жегалкина общего вида в виде двоичного вектора всех 2n коэффициентов значений конъюнкций полинома, при этом неиспользуемые s конъюнкций в первой цепочке и r конъюнкций во второй цепочке оказываются приравненными нулю.