Геодезическая призма для отклонения пучка монохроматических поверхностных плазмон-поляритонов терагерцового диапазона

Геодезическая призма для отклонения пучка монохроматических поверхностных плазмон-поляритонов терагерцового диапазона

Иллюстрации

Показать все

Реферат

Изобретение относится к области передачи и получения информации посредством поверхностных плазмон-поляритонов (ППП) - разновидности поверхностных электромагнитных волн (ПЭВ), существующих на поверхности материалов с отрицательной диэлектрической проницаемостью - терагерцового (ТГц) диапазона, и может найти применение в спектроскопии проводящей поверхности, в электронно-оптических устройствах передачи и обработки информации, в инфракрасной (ИК) технике.

С созданием перестраиваемых по частоте (в том числе и в ТГц-диапазоне) лазеров на свободных электронах, квантово-каскадных лазеров, а также импульсных лазеров, генерирующих широкополосное ТГц излучение, началось интенсивное освоение ТГц области спектра (Bründermann E., Hübers H.-W. and Kimmitt M.F. Terahertz Techniques // Springer series in optical Sciences, v.151. Springer-Verlag Berlin Heidelberg, 2012. - 383 p.) [l]. Одной из важных областей использования ТГц-излучения является спектроскопия поверхности твердого тела, а также передача информации посредством ПЭВ, к классу которых относятся и поверхностные плазмон-поляритоны на границе "металл-диэлектрик" (Maier S.A. Plasmonics: Fundamentals and Applications // Springer Science + Business Media LLC, 2007. - 223 p.) [2].

В устройствах (спектрометрах, рефрактометрах, датчиках), в которых в качестве носителя информации используют ТГц ППП, важной проблемой является отклонение пучка ППП от исходного направления распространения на тот или иной угол с целью либо отделения пучка от паразитных объемных волн (Gerasimov V.V., Knyazev B.A., Nikitin A.K., Nikitin V.V. Method for identifying diffraction satellites of surface plasmons in terahertz frequency range // Technical Physics Letters, 2010, V.36, No.11, p.1016-1019) [3], либо для сбивания измерительного пучка с опорным в плазменных интерферометрах и датчиках (Жижин Г.Н., Кирьянов А.П., Никитин A.K., Хитров О.В. Дисперсионная Фурье-спектроскопия поверхностных плазмонов инфракрасного диапазона // Оптика и спектроскопия, 2012, Т.112, №4, с.597-602.) [4], либо для определения показателя преломления ППП (Богомолов Г.Д., Жижин Г.Н., Кирьянов А.П., Никитин A.K., Хитров О.В. Определение показателя преломления поверхностных плазмонов ИК-диапазона методом статической асимметричной интерферометрии // Известия РАН. Серия физическая, 2009, Т.73, №4, с.562-565.) [5].

Наиболее близким по технической сущности к заявляемому устройству является описанная в патенте РФ на изобретение №2352969 [6] геодезическая призма для отклонения пучка монохроматических ТГц ППП, выполненная на плоской поверхности образца, направляющей ППП, в виде имеющей сглаженные края и пересекающей пучок правильной конусной канавки, ось которой лежит в плоскости поверхности образца и перпендикулярна направлению распространения ППП, а размер канавки в направлении распространения пучка меньше длины распространения ППП, при этом угол отклонения пучка равен:

γ = arcsin [ t g ( α ) ⋅ ( π − 2 ) ⋅ κ ' ] ,         ( 1 )

где α - угол между образующей и осью конуса, κ′ - действительная часть показателя преломления ППП [6] (Bogomolov G.D., Zhizhin G.N., Nikitin A.K., Knyazev B.A. Geodesic elements to control terahertz surface plasmons // Nuclear Instruments and Methods in Phys. Research (A), 2009, V.603, No.1/2, p.52-55) [7]. Основными недостатками известной призмы являются ее низкая эффективность, большие габариты, материалоемкость и трудозатраты, необходимые для ее изготовления. Все перечисленные недостатки обусловлены необходимостью принадлежности оси призмы поверхности образца для обеспечения неизменности линейной формы волнового фронта пучка ППП после прохождения им призмы. При этом глубина канавки достигает макроскопических размеров (сантиметров), что и приводит к большим габаритам, материалоемкости и трудозатратам, а также к большим радиационным потерям ППП на ребрах (краях) канавки.

Техническим результатом, на достижение которого направлено изобретение, является повышение эффективности устройства, а также уменьшение его габаритов, снижение материалоемкости и трудозатрат, необходимых для его изготовления.

Технический результат достигается тем, что геодезическая призма для отклонения пучка монохроматических поверхностных плазмон-поляритонов (ППП) терагерцового диапазона, выполненная на плоской поверхности образца, направляющей ППП, в виде имеющей сглаженные края и пересекающей пучок правильной конусной канавки, ось которой параллельна поверхности образца и перпендикулярна направлению распространения ППП, а размер канавки в направлении пучка меньше длины распространения ППП, имеет ось, проходящую над поверхностью образца, причем края канавки совпадают с прямолинейными частями линии пересечения поверхности образца и поверхности конуса канавки.

Повышение эффективности работы призмы достигается за счет уменьшения радиационных потерь ППП на ее ребрах (краях), поскольку подъем оси канавки над плоскостью образца позволяет увеличить средний радиус кривизны поверхности призмы, что, в свою очередь, делает возможным увеличение радиуса закругления ребер и, как следствие этого, - уменьшение дифракционных потерь ППП на краях призмы.

Снижение материалоемкости и трудозатрат, необходимых для изготовления призмы, а также уменьшение ее габаритов достигается вследствие уменьшения глубины канавки при нахождении ее оси не в плоскости поверхности образца, а над ней.

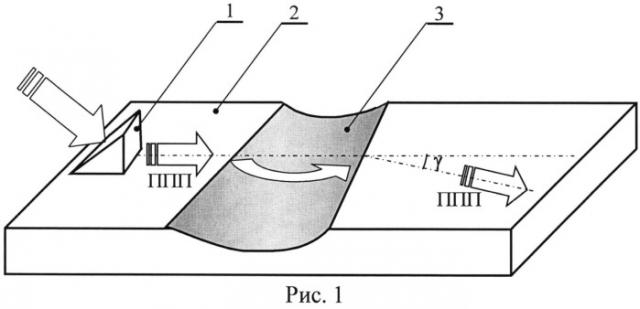
На Рис.1 приведена схема заявляемого устройства, где использованы следующие обозначения: 1 - элемент преобразования объемного излучения в ППП; 2 - плоская поверхность образца, направляющая ППП; 3 - геодезическая призма, ось которой находится над поверхностью 2.

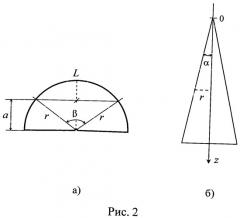
На Рис.2 - вспомогательные схемы, иллюстрирующие вывод формулы (2) для расчета зависимости геометрического пути L-лучей пучка ППП от расстояния z между проекцией трека данного луча на ось правильного конуса, содержащего поверхность призмы 3, и его вершиной.

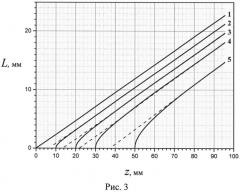
На Рис.3 приведены расчетные зависимости геометрического пути L-лучей параллельного пучка ППП по поверхности геодезической призмы 3 от расстояния z между проекцией трека данного луча на ось конуса, содержащего поверхность призмы 3, и его вершиной при различных расстояниях а от оси конуса до поверхности 2: кривая 1 - при a=0; 2-a=10 мм; 3-a=20 мм; 4-a=30 мм; 5=a=50 мм.

Заявляемое устройство работает следующим образом. Элемент 1 преобразует падающий на него коллимированный пучок объемного монохроматического излучения в пучок лучей ППП, имеющий линейный волновой фронт и распространяющийся по поверхности 2 образца. Достигнув переднего (по ходу излучения) края призмы (канавки) 3, лучи пучка устремляются по ее конической поверхности, сохраняя исходное направление своего распространения. Поскольку расстояние L, проходимое лучами в призме 3, зависит от расстояния z между вершиной конуса, содержащего поверхность канавки, и проекцией трека данного луча на ось конуса, то противоположного края призмы 3 лучи пучка достигают не одновременно, а с некоторым запаздыванием Δt(z) относительно ближайшего к вершине конуса луча. В [7] показано, что если зависимость L(z) линейна, то и зависимость Δt(z) также имеет линейный характер, что и приводит к повороту волнового фронта пучка на угол γ, рассчитываемый по формуле (1). Так обеспечивается отклонение пучка лучей ППП от исходного направления распространения.

Докажем, что условие линейности зависимости L(z) обеспечивается и в случае, если ось конуса, поверхность которого содержит поверхность канавки, находится над плоскостью образца, а не принадлежит ей. Известно, что сечение правильного конуса плоскостью, параллельной его основанию, есть окружность, а длина дуги L окружности, ограниченной двумя радиусами r этой окружности, равна: L=r·β, где β - угол между этими радиусами, выраженный в радианах. Из Рис.2(a) видно, что cos(β/2)=a/r, откуда β=2·arccos(a/r), где а - расстояние от оси конуса до поверхности 2, направляющей ППП. В свою очередь, из Рис.2(б) следует, что tg(α)=r/z, откуда r=z·tg(α); здесь z - координата содержащего данный луч пучка поперечного сечения конуса. Подставив выражения для r и β в формулу для L, получим следующий вид зависимости L(z):

На первый взгляд зависимость L(z) является нелинейной, но ее математический анализ показывает, что существенная нелинейность имеет место только при значениях a, близких к z; причем, чем больше величина a, тем больше это отличие. При малых же a отличие зависимости L(z) от линейной существенно (для деформации волнового фронта пучка ППП) только при z→a, а при a=0 это отличие исчезает полностью.

В качестве примера применения заявляемого устройства рассмотрим возможность отклонения с его помощью пучка шириной 10 мм монохроматических ППП с длиной волны λ=130 мкм на угол γ=5° при распространении пучка по плоской поверхности размещенного в воздухе золотого образца шириной 30 мм. В этом случае действительная часть показателя преломления ППП κ′≈1,0003, а длина распространения ППП достигает 10 метров, что во много раз превышает размер призмы в направлении распространения пучка. Тогда из формулы (1) следует, что для отклонения пучка на 5° угол α при вершине конуса призмы должен быть равен 4°22′. На Рис.3 приведены рассчитанные для рассматриваемого примера зависимости L(z) при различных значениях расстояния a. Видно, что, например, при a=20 мм (кривая 3) зависимость L(z) становится линейной при z>30 мм. Тогда, выбрав участок шлифовального конуса с 30 мм≤z≤60 мм, в плоскогранном образце (подложке) можно сформировать геодезическую призму, имеющую максимально заглубленные точки на боковых гранях (параллельных треку ППП) образца 1,5 мм и 4,5 мм соответственно. Такая призма будет обеспечивать поворот волнового фронта пучка ППП на 5°, не нарушая его линейности. Для достижения этого же результата с помощью призмы, ось которой принадлежала бы плоскости образца (а не располагалась бы над ней, как в приведенном примере), потребовалось бы заглубиться в образец не менее чем на 22,25 мм (при условии, что вершина конуса находится на ребре, образованном противоположной боковой гранью образца и его поверхностью, направляющей пучок). Выигрыш (по габаритам, весу, материалоемкости и трудоемкости), обеспечиваемый заявляемой призмой по сравнению с призмой-прототипом, очевиден. Кроме того, формирование призмы шлифовальным конусом с большим радиусом позволяет закруглить ребра призмы сопряжениями, имеющими также больший радиус, что позволяет уменьшить радиационные потери ППП, а следовательно, повысить эффективность работы призмы.

Таким образом, по сравнению с прототипом заявляемое устройство обладает более высокой эффективностью, а также имеет меньшие габариты, материалоемкость и необходимые для его изготовления трудозатраты, что достигается в результате уменьшения глубины конической канавки, образующей призму, отклоняющую пучок ППП на один и тот же угол, при расположении ее оси не в плоскости поверхности образца, а над ней.

Источники информации, принятые во внимание при составлении заявки:

1. Bründermann E., Hübers H.-W. and Kimmitt M.F. Terahertz Techniques // Springer series in optical Sciences, v.151. Springer-Verlag Berlin Heidelberg, 2012. - 383 p.

1. Maier S.A. Plasmonics: Fundamentals and Applications // Springer Science + Business Media LLC, 2007. - 223 p.

2. Gerasimov V.V., Knyazev B.A., Nikitin A.K., Nikitin V.V. Method for identifying diffraction satellites of surface plasmons in terahertz frequency range // Technical Physics Letters, 2010, V.36, No.11, p.1016-1019.

3. Жижин Г.Н., Кирьянов А.П., Никитин A.К., Хитров О.В. Дисперсионная Фурье-спектроскопия поверхностных плазмонов инфракрасного диапазона // Оптика и спектроскопия, 2012, Т.112, №4, с.597-602.

4. Богомолов Г.Д., Жижин Г.Н., Кирьянов А.П., Никитин A.К., Хитров О.В. Определение показателя преломления поверхностных плазмонов ИК-диапазона методом статической асимметричной интерферометрии // Известия РАН. Серия физическая, 2009, Т.73, №4, с.562-565.

5. Жижин Г.Н., Никитин A.К., Никитин П.А. Способ разделения совмещенных поверхностной и объемной электромагнитных волн терагерцового диапазона // Патент РФ на изобретение №2352969. - Бюл. №11 от 20.04.2009 г. (прототип).

6. Bogomolov G.D., Zhizhin G.N., Nikitin A.K., Knyazev B.A. Geodesic elements to control terahertz surface plasmons // Nuclear Instruments and Methods in Phys. Research (A), 2009, V.603, No.1/2, p.52-55.

Геодезическая призма для отклонения пучка монохроматических поверхностных плазмон-поляритонов (ППП) терагерцового диапазона, выполненная на плоской поверхности образца, направляющей ППП, в виде имеющей сглаженные края и пересекающей пучок правильной конусной канавки, ось которой параллельна поверхности образца и перпендикулярна направлению распространения ППП, а размер канавки в направлении пучка меньше длины распространения ППП, отличающаяся тем, что ее ось, находится над поверхностью образца, причем края канавки совпадают с прямолинейными частями линии пересечения поверхности образца и поверхности конуса канавки.