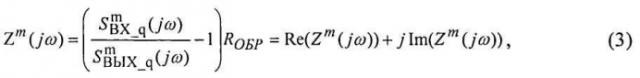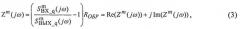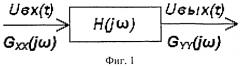Способ измерения параметров элементов многоэлементных нерезонансных линейных двухполюсников

Способ измерения параметров элементов многоэлементных нерезонансных линейных двухполюсников

Иллюстрации

Показать все

Реферат

Изобретение относится к технике измерения параметров элементов электрических цепей и может быть использовано для измерения параметров элементов многоэлементных двухполюсников, в том числе параметров элементов эквивалентных схем замещения полупроводниковых приборов.

Известен способ определения параметров элементов многоэлементных двухполюсников, заключающийся в том, что на полюса контролируемого двухполюсника, состоящего из n элементов с неизвестными параметрами, и на полюса эталонного двухполюсника, например резистора сопротивлением R_ЭТ, поочередно подают синусоидальное напряжение на n частотах, измеряют комплексный ток через контролируемый двухполюсник и эталон на n частотах и по фиксированным результатам измерения на каждой из n заданных частот, используя информацию об амплитуде комплексных токов, производят расчет параметров контролируемого двухполюсника по схеме его замещения путем решения соответствующей системы уравнений (см. Патент №2260809 РФ G01R 27/14).

Недостатком известного способа является большое время измерения, обусловленное необходимостью поочередного измерения комплексных токов через контролируемый двухполюсник и эталонный двухполюсник на n различных частотах.

Известно (см. Кнеллер В.Ю., Боровских Л.П. Определение параметров многоэлементных двухполюсников. - М.: Энергосггокиздат, 1986. - 144 с.), что погрешность определения параметров элементов двухполюсника сильно зависит от выбора частот тестового сигнала, для которых составляется и решается система уравнений, и при произвольном (неоптимальном) выборе частот может достигать десятков процентов. В общем случае для определения параметров элементов произвольного n-элементного двухполюсника с известной эквивалентной схемой замещения в отсутствие априорной информации о диапазоне изменения параметров его элементов необходимо измерять параметры импеданса двухполюсника во всем возможном диапазоне частот.

Известен способ измерения импеданса пассивного двухполюсника на заданной частоте путем измерения протекающего через двухполюсник переменного тока при подсоединении двухполюсника к генератору известного переменного напряжения (Мирский Г.Я. Электронные измерения. - М.: Радио и связь, 1986. - 440 с.). В известном способе с генератора синусоидального напряжения подают сигнал заданной амплитуды U₀ и частоты на измеряемый двухполюсник с неизвестным комплексным импедансом Z ˙ , преобразователь ток-напряжение формирует пропорциональное комплексному току через двухполюсник I ˙ напряжение, которое измеряет фазочувствительный вольтметр. Комплексный импеданс получают по закону Ома: Z ˙ = U I ˙ .

Недостатком известного способа является большое время измерения, обусловленное необходимостью проводить измерения на нескольких частотах переменного напряжения, и невысокая точность, поскольку параметры двухполюсника определяются из решения системы нелинейных уравнений, точность решения которой определяется выбором частот измерения.

Прототипом предлагаемого способа является способ оценивания амплитудных и фазовых характеристик систем по наблюдениям входных и выходных случайных процессов (см. Бендат Дж., Пирсол А. Применения корреляционного и спектрального анализа: Пер. с англ. - М.: Мир, 1983. - 312 с.). Суть способа заключается в том, что на вход системы, имеющей комплексную частотную характеристику H(jω), подается случайный процесс U_BX(t) со спектральной плотностью мощности G_XX(jω), на выходе системы регистрируется случайный процесс U_ВЫХ(t) со спектральной плотностью мощности G_YY(jω) (фиг.1) и частотная характеристика системы определяется из соотношения:

H(jω)=|H(ω)|e^-jφ(ω)=G_XY(jω)/G_XX(jω),

где |Н(ω)| и φ(ω) - амплитудная и фазовая частотные характеристики системы соответственно; G_XY(jω) - взаимная спектральная плотность мощности входного и выходного случайных процессов.

В данном методе оценивания под случайным процессом подразумевается множество (ансамбль) функций времени. Как известно (см. Гоноровский И.С. Радиотехнические цепи и сигналы. - М.: Радио и связь, 1986. - 512 с.) усреднение по ансамблю амплитудного и фазового спектров реализаций, получаемых прямым Фурье-преобразованием, приводит к нулевому спектру процесса из-за случайности и независимости фаз спектральных составляющих в различных реализациях. В связи с этим для оценки характеристик случайных процессов используется спектральная плотность мощности случайного процесса. Однако если провести одновременную запись входного U_BX(t) и выходного U_ВЫХ(t) сигналов, например, с использованием ЭВМ, и после этого осуществлять их математические преобразования, то такие сигналы можно считать детерминированными, и для анализа прохождения сигнала через систему (в случае ее линейности) можно использовать спектральный метод анализа прохождения детерминированного сигнала через линейные цепи, тем самым сокращая время вычисления (см. Гоноровский И.С. Радиотехнические цепи и сигналы. - М.: Радио и связь, 1986. - 512 с.).

Технический результат - сокращение времени измерения параметров эквивалентных схем замещения многоэлементных линейных двухполюсников.

Технический результат достигается тем, что на контролируемый n-элементный двухполюсник подают напряжение в виде случайного сигнала, имеющего равномерный амплитудный спектр в диапазоне частот, перекрывающем диапазон частот, за пределами которого модуль импеданса двухполюсника можно считать не зависящим от частоты с заданной погрешностью, и на образцовом резисторе, включенном последовательно с двухполюсником, измеряют напряжение, пропорциональное току двухполюсника, по двум параллельным каналам записывают в память ЭВМ временные реализации сигналов, подаваемого на двухполюсник и снимаемого с образцового резистора, после чего рассчитывают спектральные плотности напряжения и тока, рассчитывают частотные зависимости модуля и фазы импеданса двухполюсника, определяют характерные частоты, составляют и решают систему из n уравнений относительно параметров эквивалентной схемы замещения n-элементного линейного двухполюсника.

Сущность способа состоит в следующем.

Шумовой сигнал U_BX(t) с равномерным амплитудным спектром подается на делитель, составленный из контролируемого n-элементного линейного двухполюсника и образцового токосъемного резистора сопротивлением R_ОБР, и параллельно подается на первый канал устройства сбора данных. При измерении параметров эквивалентной схемы полупроводниковых диодов, представляемых двухполюсником, задается рабочая точка (I₀; U₀) от дополнительного источника смещения. С образцового резистора снимается выходной сигнал U_ВЫХ(t) и подается на второй канал устройства сбора данных. Сигналы U_BX(t) и U_ВЫХ(t) подвергаются аналого-цифровому преобразованию и сохраняются в память компьютера в виде дискретной последовательности отсчетов U_BX(iΔt) и U_ВЫХ(iΔt), где интервал Δt определяется частотой дискретизации: Δt=1/F_Д. Известно, что снизить погрешность оценивания спектральной плотности шумового сигнала можно путем усреднения оценок по ансамблю (см. Бендат Дж., Пирсол А. Применения корреляционного и спектрального анализа: Пер. с англ. - М.: Мир, 1983. - 312 с.). Поскольку белый шум является стационарным эргодическим процессом, то ансамбль реализаций можно получить путем разбиения (в том числе, с перекрытием по времени) исходных последовательностей отсчетов U_BX(iΔt) и U_ВЫХ(iΔt) на K последовательностей U B X m ( i Δ t ) и U В Ы Х m ( i Δ t ) (1≤m≤K), состоящих из N отсчетов и имеющих длительность (N-1)Δt каждая. Применяя прямое Фурье-преобразование к каждой последовательности, получают K комплексных спектральных плотностей входного и выходного сигналов:

Для каждой m-й реализации ансамбля рассчитывается импеданс двухполюсника:

после чего вычисляются модуль и фаза импеданса:

Затем проводится усреднение полученных частотных характеристик по ансамблю:

Расчет параметров {X_i} n-элементного двухполюсника осуществляется на основании информации о структуре эквивалентной схемы двухполюсника путем составления и решения системы из n уравнений вида:

где Ф(ω,X) и Ψ(ω,X) - функциональные зависимости модуля и фазы импеданса от частоты и параметров элементов двухполюсника соответственно. С целью минимизации погрешности определения параметров n-элементного двухполюсника, обусловленной случайной погрешностью измерения частотных зависимостей модуля и фазы импеданса, частоты ω_k и ω_l выбираются в характерных точках частотной зависимости модуля и фазы импеданса: минимум фазы, точка перегиба модуля импеданса (см., например, A. Wadsworth. The Parametric Measurement Handbook. Third Edition. - USA: Agilent Technologies, Inc. 2012. - 214 p.) или определяются по алгоритму нахождения оптимальных частот (см. Кнеллер В.Ю., Боровских Л.П. Определение параметров многоэлементных двухполюсников. - М.: Энергоатомиздат, 1986. - 144 с.). В общем случае частоты ω_k и ω_l могут совпадать, поэтому n/2≤k+l≤n.

При использовании гармонического сигнала для сканирования импеданса двухполюсника в частотном диапазоне ΔF с фиксированным разрешением по частоте Δf минимальное время сканирования составляет T   С К А Н _ Г А Р М = Δ F Δ f 2 . Минимальное время сканирования импеданса двухполюсника предложенным способом определяется нижней частотой заданного диапазона ΔF: T   С К А Н _ Ш У М = 1 Δ f . Таким образом, выигрыш по времени сканирования составляет Δ F Δ f .

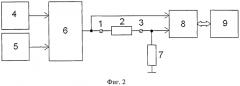
Способ может быть реализован с помощью устройства, структурная схема которого показана на фиг.2. Устройство содержит две клеммы 1 и 3 для подключения контролируемого двухполюсника 2, источника шумового сигнала 4, источника напряжения смещения 5, сумматора напряжений 6, образцового резистора 7, двухканального блока аналого-цифрового преобразования 8 и компьютера 9.

Шумовой тестовый сигнал U_Ш(t) с выхода генератора шума 4 и постоянное напряжение смещения U₀ от источника напряжения смещения 5 поступают на сумматор напряжений 6. С выхода сумматора напряжений 6 напряжение U_BX(t)=U_Ш(t)+U₀ подается на делитель, составленный из исследуемого двухполюсника 2 и образцового резистора 7 с сопротивлением R_ОБР. Параллельно по опорному каналу напряжение U_BX(t) поступает на первый канал блока аналого-цифрового преобразования 8. С токосъемного резистора R_ОБР напряжение U_ВЫХ(t) поступает на второй канал блока аналого-цифрового преобразования 8. По сигналу запуска производится измерение сигналов U_BX(t) и U_ВЫХ(t) и пересылка оцифрованных данных U_BX(iΔt) и U_ВЫХ(iΔt) в компьютер, где осуществляется расчет параметров элементов n-элементного двухполюсника по изложенному алгоритму.

Сопротивление образцового резистора R_ОБР выбирается из условия R_ОБР<<|Z(ω)| во всем диапазоне частот, при этом величина сопротивления R_ОБР должна быть такой, чтобы обеспечить требуемую чувствительность блока аналого-цифрового преобразования.

Способ измерения параметров элементов многоэлементных нерезонансных линейных двухполюсников, состоящий в том, что на контролируемый n-элементный двухполюсник подают напряжение в виде случайного сигнала, имеющего равномерный амплитудный спектр в диапазоне частот, перекрывающем диапазон частот, за пределами которого модуль импеданса двухполюсника можно считать не зависящим от частоты с заданной погрешностью, и на образцовом резисторе, включенном последовательно с двухполюсником, измеряют напряжение, пропорциональное току двухполюсника, по двум параллельным каналам записывают в память ЭВМ временные реализации сигналов, подаваемого на двухполюсник и снимаемого с образцового резистора, после чего рассчитывают спектральные плотности напряжения и тока, рассчитывают частотные зависимости модуля и фазы импеданса двухполюсника, определяют характерные частоты, составляют и решают систему из n уравнений относительно параметров эквивалентной схемы замещения n-элементного линейного двухполюсника.