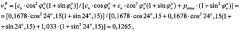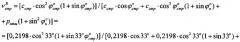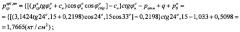Способ определения модуля деформации материальной среды

Способ определения модуля деформации материальной среды

Иллюстрации

Показать все

Реферат

Изобретение относится к области «Физики контактного взаимодействия» изотропной материальной среды, конкретно к способу определения ее модуля общей и упругой деформации.

Известен способ определения модуля E деформации материальной среды, заключающийся в том, что горизонтально устанавливают на глубине h в шурфе-дудке массива среды при доступе всестороннего атмосферного нейтрального давления плоский жесткий штамп заданного размера в×l (см×см) прямоугольной или круглой формы диаметром d (см), материальную среду через штамп вертикально нагружают возрастающими ступенями статического эффективного избыточного давления Δp_i (кГ/см²), замеряют во времени t до стабилизации соответствующие значения осадок S_i=f(Δp_i,t), строят график испытания среды S_i=f(Δp_i-const,t) или p_i=f(ΔS_i-const,t), модуль общей деформации среды при ее испытании статическими нагрузками определяют по зависимости , где ω - коэффициент формы и жесткости штампа, В - ширина или диаметр штампа (см), ν₀ - коэффициент (Пуассона) общей относительной поперечной деформации среды, ΔS - интервал общей (остаточной и упругой) осадки штампа в пределах условно линейной зависимости между осадками S_i и давлением p_i [1, 2], а модуль упругой деформации среды определяют как [3], где S₀ - начальная (мгновенная) осадка среды под начальным давлением p₀=p_ср-0,1γh (кГ/см²), где p_ср - среднее давление на среду (кГ/см²), γ - удельный вес среды (кг/см³).

Недостатком известного способа определения модулей деформации среды жестким горизонтальным штампом в шурфе-дудке является: 1) произвольный выбор условно линейного участка графика S_i=f(p_i) деформации среды под давлением; 2) установки точного значения коэффициента ω формы и жесткости штампа для разновидностей среды и различной формы и жесткости штампа только опытным путем; 3) определение коэффициента ν Пуассона с весьма приближенным значением, не отражающим конкретные условия работы среды под штампом, когда среда должна находиться в упругом структурированном состоянии при расчете и в нарушенном упруго-вязко-пластичном состоянии при расчете ; 4) начальное давление p₀, по всей видимости, должно соответствовать гравитационному природному (бытовому) давлению p_б=p₀ среды, значение которого аналитической зависимостью известными способами не определяется; 5) при расчете модулей деформации не учитывают нейтральное атмосферное давление воздуха, оказывающего влияние на величину коэффициента бокового давления и напряженно-деформированное состояние испытываемой среды; 6) низкая точность определения модулей деформации среды методом статических нагрузок не способствует широкому внедрению нового высокопроизводительного метода испытания среды ступенями задаваемых перемещений при контроле релаксирующих в среде под штампом напряжений - метода релаксометрии.

Известен способ определения модуля E деформации материальной среды, заключающийся в том, что горизонтально устанавливают на глубине h (см) в массиве среды винтолопастной жесткий штамп диаметром d_вш (см) путем его завинчивания в среду без доступа атмосферного давления посредством колонны совмещенных наружных и внутренних труб, последние из которых жестко связывают со штампом и нагрузочным приспособлением, материальную среду через винтовую лопасть штампа вертикально нагружают возрастающими ступенями статического эффективного давления Δp_i (кГ/см²) через внутренние трубы, замеряют во времени t до стабилизации соответствующие значения осадок S_i=f(Δp_i,t), строят график испытания среды , где ν₀ - коэффициент Пуассона, k_p=f(h/d_вш) - коэффициент заглубления штампа, d_вш - диаметр штампа (d_вш=27,7 см), Δp - приращение давления на среду под штампом (кГ/см²), ΔS - соответствующее Δp приращение осадки штампа (см), Δl - поправка на осевую деформацию совмещенной колонны труб (см) [5], а модуль упругости среды под штампом определяют как , где p₀=p_ср-0,1γh (кГ/см²), γ - удельный вес среды (кг/см³), S₀ (см) - начальная осадка среды под давлением p₀ [3].

В предлагаемом способе определения модуля деформации среды в массиве винтолопастным горизонтальным штампом интервал давления Δp_i не имеет четко установленных границ и принимается ориентировочным по условно линейному графику S_i=f(p_i). Если для модуля общей деформации значение коэффициента ν₀ относится к нарушенной структуре среды, то при расчете модуля значение ν₀ должно относиться к упругой ненарушенной структуре среды. Давление среды на глубине h исследования как p₀ по предлагаемой зависимости должно соответствовать действительным параметрам гравитационного (бытового) давления p₀=p_б.

Известен способ определения модуля E деформации материальной среды, заключающийся в том, что вертикально устанавливают в обрезанных стенках скважины на глубине h (см) массива среды плоский жесткий штамп, например, двутаврового рабочего наконечника лопастного прессиометра заданного размера в×l (см×см) прямоугольной или круглой формы диаметром d (см), материальную среду в условиях доступа нейтрального атмосферного давления через штамп горизонтально нагружают возрастающими ступенями эффективного статического давления Δp_i (кГ/см²), замеряют во времени t до условной стабилизации соответствующие значения осадок S_i=f(Δp_i), строят график испытания среды S_i=f (Δp_i-const,t), модуль общей деформации среды при ее испытании статическими нагрузками или методом релаксометрии определяют по зависимости , где k - коэффициент условий работы штампа, ω - коэффициент формы и жесткости штампа, В - ширина штампа или его диаметр d (см), ν₀ - коэффициент (Пуассона) общей относительной поперечной деформации среды, ΔS (см) - интервал общей (остаточной и упругой) осадки штампа в пределах условно линейной зависимости между осадками S_i и давлением p_i [6], а модуль упругости среды определяют как , где S₀ (см) - начальная (мгновенная) осадка среды под начальным давлением p₀=p_ср-0,1γh (кГ/см²), p_ср - среднее давление на среду (кГ/см²), γ - удельный вес среды (кг/см³) [3].

Недостатком известного способа определения модуля E деформации среды вертикальным штампом в стенках скважины или вертикальной выработки является: 1) отсутствие переходного коэффициента от горизонтальных деформаций среды в зависимостях для модулей к вертикальным, а боковых горизонтальных давлений - в вертикальные через коэффициенты Пуассона ν_н и относительного бокового давления ζ_н среды с нарушенной структурой при доступе атмосферного давления; 2) отсутствие обоснования интервала давления Δp_i на условно линейном участке графика S=f(p_i), оказывающего влияние на величину ; 3) коэффициент ω определяют опытным путем для среды с различными механическими характеристиками, а в расчетах принимают его приближенные значения; 4) в расчетах модуля деформации во внимание не принимается влияние нейтрального атмосферного давления .

Известен способ определения модуля E деформации материальной среды в массиве без доступа атмосферного давления на глубине h (см) исследования лопастным прессиометром вдавливаемого или забивного типа, заключающийся в том, что материальную среду горизонтально нагружают через жесткий плоский штамп прямоугольной формы размерами B×l (см×см) или круглой формы диаметром d (см) ступенями эффективного давления Δp_i (кГ/см²), замеряют во времени t до условной стабилизации соответствующие значения осадок S=f(p_i) (см), соответствующих давлению p_i, строят график испытания среды S_i=f(Δp_i-const,t), модуль общей деформации среды определяют как [7], а модуль упругости - как , где k - коэффициент условий работы, ω - коэффициент формы и жесткости штампа, В - ширина или диаметр d (см) штампа, ν₀ - коэффициент Пуассона среды, S₀ - мгновенная осадка среды под штампом (см), p₀=p_ср-0,1γh (кГ/см²) - начальное (мгновенное) давление, γ - удельный вес среды (кг/см³), [3].

Недостатком известного способа определения модуля деформации среды в массиве является: 1) отсутствие аналитических зависимостей для точного определения коэффициентов ν₀ Пуассона среды в упругом и нарушенном состоянии; 2) отсутствие четко установленного интервала Δp_i давления для расчета модуля деформации среды; 3) принятие ориентировочного значения коэффициента ω жесткости штампа; 4) низкая точность определения значений и . Коэффициент [(1-ν₀)²/(1-2ν₀)] для и получен путем приведения полукомпрессионных условий горизонтальной работы штампа прессиометра в массиве к условиям вертикальной работы этого штампа с поверхности полупространства боковых стенок шурфа-дудки, то есть . Однако значение коэффициента ν₀ должно отвечать структурированной среде в зависимости для и нарушенной структуре среды в зависимости для с учетом пассивного предельного и в большей мере активного полукомпрессионного сжатия среды штампом.

Известен способ определения модуля E деформации материальной среды, заключающийся в том, что вертикально устанавливают на глубине h (см) массива среды через скважину радиальный эластичный трехкамерный прессиометр конструкции Л. Менара с радиусом r₀ (см), соответствующим радиусу скважины r₀=r_скв, и высотой H_пр, (см), стенки скважины пригрузочными и центральной камерами обжимают избыточным эффективным давлением, препятствующим по краям прессиометра проникновению атмосферного давления к центральной камере, а испытание среды в стенках скважины производят центральной камерой путем повышения общего давления во всех камерах и горизонтального нагружения среды в стенках скважины возрастающими ступенями статического радиального эффективного давления Δp_i (кГ/см²), замеряют приращение диаметра скважины r_i=f(p_i), строят график испытания среды центральной камерой r_i=f(Δp_i-const,t), модуль общей деформации среды при ее испытании статическими нагрузками эластичной камерой прессиометра определяют по зависимости , где Δp_i (кГ/см²) - давление камеры прессиометра на стенки скважины, ν₀ - коэффициент Пуассона среды, Δr (см) - приращение начального радиуса r₀ скважины после приложения давления, k_n - коэффициент условий испытания среды [8].

Недостатком способа определения модуля деформации среды радиальным трехкамерным прессиометром в скважине является: 1) отсутствие теоретического обоснования переходного коэффициента k_n для перевода модуля деформации, полученного упругим горизонтальным радиальным штампом прессиометра к вертикальным штамповым опытам в шурфе; 2) отсутствие определяющей зависимости для расчета коэффициента ν₀ Пуассона с учетом атмосферного давления через параметры φ° и с (кГ/см²) прочности исследуемой среды; 3) отсутствие зависимости для расчета модуля упругости среды радиальным прессиометром; 4) необходимость в рассмотрении работы трехкамерного радиального прессиометра в скважине без доступа атмосферного давления (перекрываемого крайними пригрузочными камерами) к центральной рабочей камере, которая осуществляет деформацию стенок скважины по цилиндрической поверхности (в цилиндрической системе координат) по аналогии с расширяющимся по диаметру жестким цилиндром (с развитием зон краевых сдвиговых деформаций и соответствующих им пиков контактных напряжений).

Известен способ определения модуля E деформации материальной среды, заключающийся в том, что вертикально устанавливают на глубине h (см) ниже забоя обсаженной трубами скважины в массиве среды однокамерный радиальный вдавливаемый эластичный прессиометр (типа ПВ-60), среду на глубине h обжимают возрастающими ступенями избыточного эффективного горизонтального давления Δp_i (кГ/см²) через гибкие вертикальные пластины, обкладывающие камеру прессиометра с внешней стороны, и замеряют на каждой ступени соответствующее стабилизированное во времени t приращение диаметра Δd_ц (см) центра рабочей камеры прессиометра, строят график испытания среды Δd_ц=f(Δp_i-const,t), модуль общей деформации среды в массиве определяют по зависимости , где M=0,7…0,9 - коэффициент начального напряженного состояния массива вокруг вдавливаемого цилиндрического зонда прессиометра, d_ц (см) - диаметр начального уплотнения среды под цилиндрическим телом зонда прессиометра давлением p_n (кГ/см²), Δd_ц (см) - приращение диаметра центра зонда при давлении p_k (кГ/см²), k - коэффициент [9, 10].

Недостатком известного способа определения модуля E деформации среды однокамерным прессиометром является: 1) отсутствие переводного коэффициента от горизонтального модуля деформации к требуемому вертикальному с помощью коэффициента ν₀ Пуассона; 2) необходимость в использовании вдавливаемого зонда в качестве только дополнительного прибора к обычному радиальному скважинному прессиометру при исследовании слабых водонасыщенных грунтовых сред; 3) рабочая камера вдавливаемого прессиометра при испытании среды в массиве раздувается под давлением в форму эллипсоида вращения, что необходимо учитывать в расчетной зависимости для - модуля упругости среды.

Известен способ определения модуля E деформации материальной среды в условиях гравитации (g=9,81 м/с²) и компрессионного сжатия, заключающийся в том, что на цилиндрический (в одометре) или кубический (в стабилометре типа «C») образец среды в жесткой обойме горизонтально устанавливают жесткий плоский перфорированный штамп диаметром d_к (см) или с изначальной стороной B_к (см) и площадью F_к (см²), образец среды нагружают через штамп возрастающими ступенями вертикального эффективного давления Δp_i (кГ/см²) при доступе нейтрального атмосферного давления , замеряют во времени t до условной стабилизации соответствующие значения осадок S_i=f(t) (см) среды, строят график испытания среды p_i=f(e_i) (кГ/см²) ненарушенной структуры как зависимость давления p_i от коэффициента пористости среды e_i=е₀-(1+e₀)(S_i/H_i), где начальный коэффициент пористости e₀=(γ_s-γ_d)/γ_d, γ_s (кг/см³) - удельный вес твердых частиц среды, γ_d=γ/(1+ω₀) (кг/см³) - объемный вес скелета среды; γ=ρg (кг/см³) - объемный вес среды, ω₀ - влажность среды, S_i (см) - осадка образца с начальной высотой H₀ (см), ρ (кг/см³) - плотность среды, модуль общей деформации среды в условиях компрессии определяют по зависимости , где mυ=S_i/(H_i·p_i), а коэффициент , коэффициент общей относительной поперечной деформации структурированной среды ν_стр=ε_x/ε_z (коэффициент Пуассона) [11].

Недостатками известного способа определения компрессионного модуля общей деформации среды являются: 1) испытание образцов среды только с ненарушенной структурой, отбор которых - трудоемкая операция, хотя при компрессионном испытании образец доводят под нагрузкой до состояния нарушения структуры при давлении , где (бытовое) гравитационное давление в массиве среды на глубине h равно ; 2) модуль общей деформации среды в условиях компрессионного сжатия определяют при ориентировочно принимаемом значении коэффициента ν_стр Пуассона без учета влияния атмосферного давления; 3) не учитывается в расчетах модуля влияние размера и жесткости штампа, то есть коэффициента ω; 4) при расчетах величины интервал давления Δp_i ошибочно выбирается в интервале проектируемых нагрузок от сооружения, действующего на подстилающее основание; 5) модуль упругости среды при компрессии не определяют.

Общим недостатком известных способов определения модулей деформации среды методом статических нагрузок с помощью горизонтального штампа , вертикальных штампов прессиометров , в одометрах или в стабилометрах типа «C» является существенное расхождение их показателей для одной и той же разновидности исследуемой среды, так при испытании суглинка мягкопластичной консистенции [7].

В расчетах модуля E_о общей деформации среды в массиве или в выработке плоским жестким штампом используется сомножитель , получаемый по «Теории упругости» в результате математических преобразований решения задачи о работе штампа с поверхности полупространства [12], а не через теоретическое решение задачи.

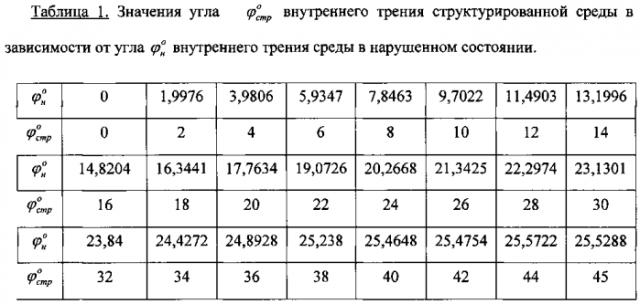
Коэффициент ν₀ Пуассона следует определять через известные расчетные зависимости с учетом параметров прочности среды φ°, с (кГ/см²), а также наличия выработки в массиве среды и доступа атмосферного давления .

В известных способах испытания торфяная среда с ненарушенной структурой ошибочно отождествляется с грунтовой упруго-вязко-пластичной средой в нарушенном состоянии и с грунтовой упругой средой в структурированном состоянии, однако в залежи торф в действительности обладает свойствами грунта только в нарушенном состоянии (искусственно переработанный торф по глубине сжимаемого массива), а в естественном состоянии - только при высокой степени разложения (R_T=45%…60%) его растительных остатков (низинная залежь). При малой степени разложения (верховая залежь) структурная прочность торфа определяется волокнами неразложившихся растительных остатков, а торф характеризуется как упруго-эластичная материальная среда (восстанавливающая объем и форму после сжатия внешней избыточной нагрузки) и определяется только модулем упругости E_упр его структурированного сложения.

Для установления истинных однозначных значений модулей деформации (общей и упругой) среды необходимо определение границ давления, определяющих ее модули, и истинной величины определяющего давления в условиях деформации среды: в массиве, с поверхности полупространства, в выработке, в условиях компрессионного и одноосного сжатия образца среды.

С целью приведения модулей деформации среды, полученных известными способами, к однозначному показателю предлагается новый способ определения модуля E_о общей деформации среды и модуля ее упругости E_упр.

Технический результат по способу определения модуля E деформации материальной среды, заключающемуся в том, что штамп с изначальной площадью F₀ (см²) устанавливают в контакте с материальной средой на глубине h (см) ее ненарушенного массива с доступом атмосферного давления ( p с р а т м = 1,033       к Г / с м 2 ) или без него, штампом на среду создают возрастающие ступени эффективного статического давления Δp_i (кГ/см²), которые выдерживают во времени t до стабилизации соответствующих значений осадок среды S_i (см) под штампом, регистрируют результаты испытания среды ΔS_i=f(Δp_i-const,t), устанавливают значение коэффициента Пуассона среды как ν₀=ζ₀/(1+ζ₀), где ζ₀ - коэффициент общего бокового давления среды, рассчитывают для упруго-вязко-пластичной среды (грунт, торф низинный с высокой степенью разложения R_T=45%…65% или переработанный) модуль E_о (кГ/см²) общей деформации, достигается тем, что по предварительно отобранным с глубины h образцам среды с ненарушенной структурой для расчета модуля деформации определяют ее удельный вес γ_стр (кг/см³) и параметры прочности - угол внутреннего трения и удельное сцепление c_стр (кГ/см²), в нарушенном состоянии параметры прочности среды определяют как , c_н=c_стр[2-tgφ_н/tgφ_стр] (кГ/см²), рассчитывают величины эффективного гравитационного (бытового) давления в структурированной среде как p б с т р = c с т р t g φ с т р о       ( к Г / с м 2 ) и в среде с нарушенной структурой как p б н = c н t g φ н о       ( к Г / с м 2 ) , эффективного начального (первого) критического давления сжатия образца среды в условиях компрессии p с р к = p с р , с ж к р 1 = [ p а т м ( 1 + sin φ н о ) + 2 c н cos φ н о ] / ( 1 − sin φ н о )       ( к Г / с м 2 ) и коэффициентов Пуассона среды в массиве - как и , в стенках выработки как - и , в условиях компрессионного сжатия - как и , испытания среды под штампом S_i=f(p_i) статическими нагрузками Δp_i производят при создании на среду давления, равного гравитационному (бытовому) давлению, разгрузку среды до нулевого давления p₂=0 (кГ/см²), нагружении среды давлением p 3 = p б н       ( к Г / с м 2 ) и давлением p 4 = p с р к р 1       ( к Г / с м 2 ) при замере стабилизированных во времени t соответствующих значений осадок среды , а модуль общей деформации упруго-вязко-пластичной среды (грунт, торф низинный с высокой степенью разложения R_T=45%…65% или переработанный) определяют под горизонтальным жестким штампом с поверхности полупространства по зависимости Е.Н. Хрусталева E 0 ш т . = [ 1 − ( ν н В ) 2 ] ( B / 2 = d к р π / 4 = F к р / 2 ) [ ( p с р , с ж к р 1, п п − p б н ) / ( S к р 1 − S б н ) ]       ( к Г / с м 2 ) , где p с р , с ж . к р 1, п п = { [ ( p с р к t g φ н о + c н ) cos φ н о cos φ с т р о ] − c н } c t g φ н о − p а т м + q + p б н       ( к Г / с м 2 ) , q - давление бокового пригруза штампа (кГ/см²), а модуль упругости - по зависимости Н. Хрусталева E у п р ш т . = [ 1 − ( ν с т р . В ) 2 ] ( B = d к р π / 2 = F к р ) [ p б с т р / ( S б с т р − S 0 ) ]       ( к Г / с м 2 ) , где B - ширина (см), d_кр - диаметр (см) и F_кр - площадь (см²) круглого штампа; под горизонтальным винтолопастным штампом в массиве среды модуль общей деформации среды определяют по зависимости Е.Н. Хрусталева , где , а модуль упругости - по зависимости Е.Н. Хрусталева ; под горизонтальным штампом в шурфе-дудке или на дне вертикальной выработки модуль общей деформации среды определяют по зависимости Е.Н. Хрусталева , где , а модуль упругости - по зависимости Е.Н. Хрусталева ; под вертикальным распорным штампом лопастного прессиометра в вертикальной выработке-скважине модуль общей деформации среды определяют по зависимости Е.Н. Хрусталева , где , а модуль упругости - по зависимости Е.Н. Хрусталева ;

под вертикальным радиальным эластичным штампом радиусом r₀=r_скв в скважине радиусом r_скв трехканального прессиометра типа Л. Менара модуль общей деформации среды определяют по зависимости Е.Н. Хрусталева , а модуль упругости - по зависимости Е.Н. Хрусталева , где , l₀ - длина рабочей камеры прессиометра (см); под упругим штампом однокамерного прессиометра радиусом r₀=r_скв в скважине радиусом r_скв модуль общей деформации среды определяют по зависимости Е.Н. Хрусталева , где R^крI и R^б - большие радиусы эллипсоида эластичного штампа (см), , а модуль упругости - по зависимости Е.Н. Хрусталева , где - большой радиус эллипсоида штампа (см) при гравитационном давлении ; под горизонтальным круглым жестким перфорированным штампом d_к (см) компрессионного прибора при доступе атмосферного давления модуль общей деформации среды определяют по зависимости Е.Н. Хрусталева , где - ширина (см) прямоугольного штампа, эквивалентного круглому с площадью F_к (см²) и диаметром d_к (см), , а модуль упругости - по зависимости Е.Н. Хрусталева .

1. На базе научных достижений «Физики материального взаимодействия» подтверждено, что при превышении гравитационного (бытового) давления нарушаются структурная прочность среды в массиве и ее упругие свойства, а при достижении начальной (первой) критической нагрузки p^крI эпюры контактных напряжений под штампом шириной B в среде на 0,55B от его центра составлены из центральных упругих напряжений и на 0,25B от краев штампа составлены эпюрами напряжений пластических деформаций в сдвигаемой штампом среде. При давлении p^крI краевые контактные напряжения под штампом при отсутствии бытового давления (с поверхности полупространства) равны нулю, они максимальные от краев на 0,255B штампа и минимальные в упругой зоне под центром подошвы штампа, поэтому в определяющих зависимостях для расчета модуля общей деформации среды в интервале давлений (p^крI-p_б) принимается полуширина штампа E_о=f(B/2), а для расчета модуля упругости в интервале давлений (p_б-0) принимается полная ширина штампа E_упр=f(B).

2. Теоретически выведено и практически подтверждено значение давления p^крI под жестким плоским штампом шириной B>B_кр, большей его критического размера B_кр, принимаемого по графику S=f(B,p-varir) испытания среды. Отпадает необходимость в коэффициенте ω формы штампа в определяющих зависимостях для модулей деформации исследуемой среды.

3. Так как модуль общей деформации E_о относится к среде с нарушенной структурой, то значение должно быть переписано как и относится к коэффициенту общей относительной поперечной деформации среды с нарушенной структурой, величина которого определяется как ν_н=ζ_н/(1+ζ_н), где коэффициент общего относительного бокового давления в массиве среды с нарушенной структурой.

4. При сжатии среды в массиве в вертикальном направлении в условиях компрессионного сжатия отношение , а в условиях свободного расширения среды под штампом, например, лопастного прессиометра отношение , что и определяет выражение в зависимости для расчета модуля деформации E среды.

5. Значение коэффициента при расчете модуля общей деформации под горизонтальной плоскостью штампа переходит в коэффициент для эквивалентного ему вертикального штампа.

6. Упругое состояние материальной среды сохраняется до момента нарушения ее структурной прочности при действии гравитационного (бытового) давления .

7. При работе однокамерного радиального прессиометра радиусом r₀=r_скв в скважине радиусом r_скв эластичная оболочка при обжатии среды в стенках скважины будет при раздутии принимать форму эллипсоида вращения (x/a)²+(y/b)²+(z/c)²=1, в котором a=c=R_i, d=l/2, l (см) - длина, R_i (см) - большой радиус эллипсоида оболочки прессиометра в стенках скважины. Тогда . Объем эллипсоида вращения раздутой камеры прессиометра равен V_Эл=(4/3)πba ²=(4/3)(l/2)R²=2πlR²/3 (см³) при объеме полости окружаемой камерой скважины , тогда объем сжимаемой камерой прессиометра среды вокруг скважины будет составлять величину V_Эл=(4/3)πba ²=(4/3)(l/2)R²=2πlR²/3 (см³). Выражения для модулей деформации среды и будут определяться как

, а

,

где .

8. На графике τ_i=f(p_i) предельного состояния материальной среды Ш. Кулона, где τ_x=σ_II, τ_y=σ_III и p_i=σ_I - главные напряжения, строго направленные соответственно в горизонтальном и вертикальном направлении. Таким образом закон Ш. Кулона относится только к испытаниям среды на сжимаемость и сдвиг в компрессионных приборах и стабилометрах.

9. При определении зависимости для модуля E_о общей деформации под эластичным штампом скважинного или залавливаемого в массив корпуса радиального прессиометра следует рассматривать эластичные оболочки при (2πr₀)>l₀ и при (2πr₀)<l₀, где r₀ - начальный радиус прессиометра, l₀ - длина рабочей камеры прессиометра. По предлагаемому способу работа радиального эластичного штампа прессиометра рассматривается при (2πr₀)>l₀ как работа эквивалентного ему жесткого плоского штампа размером 2πr₀×l₀ (см×см) с поверхности полупространства, при этом площади эластичного штампа прессиометра и эквивалентного ему плоского штампа равны F_пр=F_шт=2πr₀l₀ (см²). При (2πr₀)>l₀ модуль общей деформации среды определяют для рабочег