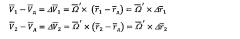Способ оценивания ошибок инерциальной информации и её коррекции по измерениям доплеровского измерителя скорости

Способ оценивания ошибок инерциальной информации и её коррекции по измерениям доплеровского измерителя скорости

Иллюстрации

Показать все

Реферат

Изобретение относится к области комплексных навигационных систем управления и наведения летательных аппаратов (ЛА).

Известен способ оптимального оценивания и коррекции инерциальной информации по измерениям горизонтальных составляющих абсолютной линейной скорости в проекциях на оси опорного трехгранника гироплатформы (ГП) инерциальной навигационной системы (ИНС).

Его описание приведено в разделе «Дополнение к задаче выставки на подвижном основании», написанном Л.Г. Клибановым и В.Л. Леонидовым, известной монографии А. Липтона «Выставка инерциальных систем на подвижном основании», «Наука», М., 1971 г. [1].

В нем рассматривается редуцированная процедура оптимального оценивания в задаче согласования ГП двух ИНС - выставляемой и базовой. Рассмотрение ведется применительно к решению задачи начальной выставки ИНС ракеты по скоростной информации, измеряемой ИНС носителя.

Однотипность измеряемых сигналов, полная адекватность математического описания модели ошибок ИНС и необходимость использования одних и тех же методических приемов повышения наблюдаемости делают рассматриваемый способ по своей технической сущности достаточно близким к предлагаемому способу коррекции по измерениям доплеровского измерителя составляющих скорости (ДИСС), что позволяет принять его в качестве наиболее близкого аналога.

Формализуя приведенное в [1] его описание, приведем его в следующем виде:

Способ оценивания ошибок инерциальной информации и ее коррекции по измерениям ДИСС основанный на процедуре оптимальной фильтрации и идентификации скоростных сигналов измерения, которые формируют путем сравнения горизонтальных составляющих абсолютной линейной скорости, измеренных ИНС, и аналогичных составляющих, сформированных по измерениям ДИСС, при этом само оценивание параметров состояния ИНС осуществляют посредством идентификации сигналов измерения, которую реализуют в соответствии с математическим описанием исходной системы, при этом полет организуют таким образом, что после 270 секунд горизонтального прямолинейного полета, осуществляют маневр, типа «змейки», координированного или боевого разворотов, после чего активную фазу процедуры оптимальной фильтрации и идентификации дискретной последовательности сигналов измерения приостанавливают и фильтр-идентификатор переводят в режим долгосрочного - до следующего сеанса коррекции, прогноза с начальными условиями, определяемыми значениями оценок на момент завершения активной фазы оценивания, и текущими значениями параметров модели сообщения, при этом коррекцию выходных параметров ИНС - составляющих абсолютной линейной скорости, вследствие закрытости и недоступности ключевых управленческих входов каналов коррекции ИНС, осуществляют в разомкнутой схеме с использованием текущих прогнозируемых значений оценок.

Основными недостатками наиболее близкого аналога являются:

- отсутствие в математической модели ошибок ИНС дифференциальных уравнений, описывающих геометрию относительного размещения комплексируемых систем;

- при формировании матрицы наблюдения системы не учитываются погрешности Δϕ, Δλ, Δχ счисления основной тройки навигационных параметров в функции малых углов α_х, α_y, α_z ухода реальной ГП ИНС;

- при выполнении традиционных для рассматриваемого режима коррекции маневров, типа «змейки», координированного или боевого разворотов, вместо ожидаемого, эффективного оценивания всех параметров состояния и, в первую очередь, слабонаблюдаемых, таких, как угол α_z азимутального ухода ГП и дрейф ε_y гироскопа продольного канала, с целью чего и осуществляется маневр, имеет место абсолютно обратная картина расходимости последних и на рушение сходимости остальных;

- не характерные для процедуры оптимального оценивания точность и быстродействие, что является показателем неэффективности оптимальной обработки и коррекции в целом.

Технический результат предлагаемого изобретения - повышение точности и быстродействия оптимального оценивания и коррекции всех измеряемых инерциальной системой параметров в обеспечение эффективного решения навигационных, боевых и специальных задач.

Указанный технический результат достигается за счет того, что в способе оценивания ошибок инерциальной информации и ее коррекции по измерениям доплеровского измерителя скорости, включающем использование классической дискретной процедуры оптимальной фильтрации и идентификации Калмана, для чего входные сигналы оптимального фильтра-идентификатора формируют путем сравнения одноименных горизонтальных составляющих абсолютной линейной скорости, измеренных ИНС и сформированных по измерениям ДИСС, а его структуру синтезируют в соответствии с традиционной для ИНС моделью ошибок, при этом характер полета методически организуют таким образом, что после 270-ти секунд горизонтального прямолинейного полета, на котором реализуют точное «горизонтирование» и оценивают хорошо наблюдаемые параметры горизонтальных каналов ИНС, осуществляют маневр, типа «змейки», координированного или боевого разворотов, после чего активную фазу процедуры оптимальной фильтрации и идентификации приостанавливают и фильтр-идентификатор переводят в режим долгосрочного, до следующего сеанса коррекции, прогноза, для реализации которого сигналы измерения и оптимальные коэффициенты усиления фильтра-идентификатора обнуляют, а значения оценок на момент завершения активной фазы процедуры оценивания используют в качестве начальных условий в процедуре прогноза, при этом сам прогноз осуществляют в соответствии с дискретными уравнениями для расчета априорных оценок ошибок ИНС, а коррекцию выходных параметров ИНС реализуют в разомкнутом контуре, для чего используют текущие прогнозируемые значения оценок, дополнительно, разработанную для рассматриваемого режима коррекции модель ошибок ИНС расширяют за счет включения в нее математического описания координат ее местоположения (размещения) относительно ДИСС, и представляют его в виде системы из трех взаимосвязанных дифференциальных уравнений первого порядка в проекциях на оси опорного трехгранника ГП ИНС, которые одновременно описывают и аддитивно входящие в сигналы измерения составляющие кинематической скорости ИНС относительно ДИСС, и дополнительно, при формировании матрицы наблюдения используют кинематические соотношения, связывающие ошибки Δϕ, Δλ, Δχ счисления географических координат местоположения и угла азимутальной ориентации опорного трехгранника ГП ИНС, с погрешностями выдерживания вертикали α_х, α_y и углом α_z азимутального ухода ГП, которые, с точностью до величин второго порядка малости относительно малых величин α_х, α_y, α_z, Δλ определяют все элементы матрицы наблюдения, чем обеспечивают точное и эффективное оценивание и прогноз таких ошибок автономного инерциального счисления, как ΔV_x, ΔV_y, α_х, α_у, α_z, Δξ, Δη, Δζ, при этом коррекцию счисленных инерциальной системой географических координат местоположения и угла азимутальной ориентации опорного трехгранника ее ГП реализуют, используя текущие спрогнозированные значения оценок малых углов , , рассогласования реального и опорного трехгранников ГП ИНС и счисленные/откорректированные значения географической широты и угла азимутальной ориентации опорного трехгранника ГП ИНС и, в соответствии с кинематическими соотношениями связи Δϕ, Δλ, Δχ с малыми углами α_х, α_у, α_z текущего ухода реальной ГП ИНС, последовательно формируют оценки ошибок , , счисления основных навигационных параметров и последовательно корректируют счисленные значения географических координат , местоположения и истинного курса ориентации опорного трехгранника ГП ИНС, а для выявления из двух потенциально равноточных ИНС той, угловая информация которой наиболее приемлема для пилотирования и решения боевых и специальных задач, а также для коррекции текущих значений углов тангажа , крена , и гироскопического курса используют текущие спрогнозированные значения оценок малых углов , , рассогласования реального и опорного трехгранников ГП ИНС и измеренные/откорректированные значения углов тангажа и гироскопического курса и, в соответствии с кинематическими соотношениями связи ошибок , Δγ, Δψ_г измерения углов ориентации объекта с малыми углами α_х, α_у, α_z текущего ухода реальной ГП ИНС, последовательно для каждой ИНС формируют текущие значения оценок ошибок измерения углов ориентации объекта , , и рассчитывают текущие значения сумм их квадратов , посредством сравнения которых выявляют минимальную из них и, тем самым определяют наиболее приемлемую для решения обозначенных задач ИНС, а, при необходимости, последовательно корректируют измеренные значения углов тангажа , крена , и гироскопического курса в соответствии с последовательно рассчитанными значениями оценок , , и коррекцией измеренных углов эволюции объекта по принципу «рассчитал-откорректировал», при этом откорректированное значение истинного курса объекта определяют, как сумму оценок и .

Приведем перечень и описание фигур, которые потребуются при осуществлении изобретения.

На фиг. 1 представлена схема относительного размещения на объекте ИНС1, ИНС2 и ДИСС.

В качестве параметров, определяющих размещение указанных систем на объекте приняты векторы , и , определяющие местоположение соответственно ИНС1, ИНС2 и ДИСС относительно начала (точка О) связанной с объектом системы координат (ССК) Oxyz.

На схеме также представлены векторы и , определяющие местоположение ИНС1 и ИНС2 соответственно относительно ДИСС, а также вектор положения ИНС2 относительно ИНС1.

Под ИНС2 следует понимать резервную ИНС, которая введена для общности рассмотрения.

- вектор путевой скорости объекта.

На фиг. 2 приведена взаимная ориентация географического сопровождающего трехгранника (ГСТ) ONHE и ССК Oxyz.

Их рассогласование определяется углами истинного курса , тангажа υ и крена γ объекта.

Переход от осей ГСТ ONHE к осям ССК Oxyz осуществляется посредством трех последовательных поворотов на углы , υ и γ с угловыми скоростями , и .

Приведенное на фиг. 2 направление отсчета углов , υ, γ и угловых скоростей , , является положительным.

На фиг. 3 приведена взаимная ориентация опорного трехгранника гироплатформы (ОТГП) ОξηζИНС и ССК Oxyz.

Их рассогласование определяется углами гироскопического курса , тангажа υ и крена γ объекта.

Переход от осей ОТГП Оξηζ ИНС к осям ССК Oxyz осуществляется посредством трех последовательных поворотов на углы , υ и γ с угловыми скоростями , и .

Приведенное на фиг. 3 направление отсчета углов , υ и γ и угловых скоростей , и является положительным.

На фиг. 4 приведена взаимная ориентация гринвичской системы координат (ГСК) OX'Y'Z', ОТГП ОξηζИНС и ГСТ ONHE.

Их рассогласование определяется углами географической долготы λ, широты ϕ и углом χ азимутальной ориентации ОТГП ОξηζИНС.

Переход от осей ГСК OX'Y'Z' к осям ГСТ ONHE и далее к осям ОТГП Оξηζ осуществляется посредством последовательных поворотов на углы λ и ϕ и далее на угол χ (см. фиг. 4) с угловыми скоростями , , и .

Приведенное на фиг. 4 направление отсчета углов λ, ϕ и χ и угловых скоростей , , и и их изменения следует считать положительным.

С целью раскрытия физической сути и математического содержания предлагаемых алгоритмических и математических решений приведем их подробное описание.

Но прежде - обоснование необходимости алгоритмического учета относительного размещения задействованных в инерциально-допплеровской коррекции информационных систем ИНС и ДИСС.

При разработке алгоритма оптимальной коррекции ИНС по измерениям ДИСС исключительно важное значение имеет вопрос методического обеспечения раздельного наблюдения и оценивания всех, без исключения, параметров состояния ИНС и, в первую очередь, слабоонаблюдаемых, таких, как угол α_z азимутального рассогласования реального и опорного трехгранников в гироплатформы ГП ИНС и нескомпенсированного ухода - дрейфа ε_y гироскопа продольного канала. В лабораторных условиях и для случая неподвижного объекта указанные параметры ненаблюдаемы и, как следствие, раздельно не оцениваются.

В условиях же движущегося объекта для обеспечения наблюдаемости указанных параметров нет никакой необходимости в реализации каких-то дополнительных методических решений. И это связано, исключительно, с тем, что само движение объекта является достаточно эффективным инструментом, позволяющим управлять динамикой изменения ошибок выходных параметров ИНС от всех, без исключения, параметров состояния и, как следствие, их наблюдаемостью.

При этом, чтобы обеспечить максимальную эффективность связей всех параметров состояния с выходными сигналами ИНС, такими, как географическая широта ϕ и долгота λ, и горизонтальные составляющие V_x, V_y абсолютной скорости, необходимо выполнение маневров, типа «змейки», координированного или боевого разворотов.

Выполнение упомянутых маневров, сопровождающихся достаточно интенсивным изменением угловой и пространственной ориентации объекта и, как следствие, высокодинамичным изменением составляющих его угловой и путевой скорости, при различном конструктивном размещении задействованных в рассматриваемых режимах коррекции информационных систем, приводят к появлению в сигналах измерения так называемых кинематических составляющих скорости.

Указанные составляющие скорости, будучи математически не описанными, и, как следствие, алгоритмически неучтенными, а это действительно так, вместо методически обоснованного и ожидаемого оценивания слабонаблюдаемых параметров приводят к совершенно обратному результату, а именно, к расходимости процедуры их оценивания.

Игнорирование спецификой этого явления приводит к таким выводам, типа: «курсовые ошибки хорошо оцениваются при наличии двух участков коррекции по 5…10 мин каждый, разделенных маневром по скорости и/или курсу» (см. Научно-технический журнал «Инженерная физика» №12/2012, стр. 49, 16 строка сверху).

В действительности курсовая ошибка оценивается хорошо, если она оценивается за 0,5-1 мин одного из упомянутых выше маневров.

При этом «наличие двух участков коррекции по 5…10 мин. каждый» не имеет никакого физического объяснения.

Да, для качественного оценивания параметров горизонтальных каналов ИНС необходим участок коррекции длительностью, не более 4-4,5 минут, после чего осуществляется маневр, обеспечивающий оценивание азимутальной ошибки и не ухудшающий, что особенно важно, результаты проведенного «горизонтирования».

В представленном выше случае из «Инженерной физики» маневр не только не обеспечивает оценивание азимутальной ошибки, но даже ухудшает результаты «горизонтирования», проведенного на первом 5…10-ти минутном участке коррекции.

И чтобы как-то сгладить последствия проведенного маневра, очевидно, и потребовался второй 5…10-ти минутный участок коррекции.

А теперь из общих физических представлений получим математическую модель, описывающую геометрию относительного размещения основных информационных систем на объекте, типа самолета или вертолета, и покажем, что указанная модель одновременно описывает упоминавшиеся выше кинематические составляющие скорости.

Для этого приведем вывод дифференциальных уравнений, описывающих характер изменения координат местоположения ИНС относительно ДИСС в проекциях на оси ГСТ ONHE и ОТГП ИНС Оξηζ.

Для вывода указанных дифференциальных уравнений воспользуемся схемой относительного размещения на объекте таких информационных систем, как ИНС1, ИНС2 и ДИСС, приведенной на фиг. 1.

На указанной схеме начало связанной с объектом системы координат Oxyz совмещено с центром его тяжести (ЦТ), а местоположение ИНС1, ИНС2 и ДИСС определяется векторами и . Это означает, что при векторе угловой скорости вращения объекта вокруг его ЦТ будут иметь место линейные перемещения ИНС1, ИНС2 и ДИСС со скоростями вида:

где - вектор предписанной заданием путевой скорости объекта - его ЦТ.

В соответствии с представленными на фиг. 1 векторными треугольниками О-ИНС1-ДИСС и O-ИНС2-ДИСС, запишем следующие полезные матричные равенства:

где - вектора местоположения ИНС1 и ИНС2 соответственно относительно ДИСС.

Очевидно, что сравнение скоростей перемещения ИНС1 и ИНС2 со скоростью ДИСС приведет к выражениям вида:

Из приведенных выражений следует, что скорости и движения ИНС1 и ИНС2 относительно ДИСС однозначно определяются угловой скоростью Ω' объекта вокруг его ЦТ и местоположением ИНС1 и ИНС2 относительно ДИСС Δr₁, Δr₂ (2).

Выше представлена, как угловая скорость вращения объекта вокруг ЦТ. Но этого абсолютно недостаточно для полной характеристики рассматриваемой скорости, поскольку не ясно, относительно какой системы координат следует рассматривать вращение объекта, а посему непонятна процедура ее расчета.

Для ответа на эти вопросы введем в рассмотрение абсолютную угловую скорость вращения объекта и абсолютную угловую скорость вращения географического сопровождающего трехгранника ГСТ ONHE.

Понятие абсолютной угловой скорости вращения означает вращение чего-то относительно инерциальной системы координат. В рассматриваемом случае и -это угловые скорости объекта и ГСТ ONHE относительно инерциальной системы отсчета.

Очевидно, что угловая скорость вращения объекта относительно ГСТ ONHE будет равна разности угловых скоростей и :

Учитывая, что векторы , , , жестко связанные с объектом, изменяют свои проекции на оси ГСТ ONHE, исключительно только за счет вращения связанной с объектом системы координат Oxyz относительно ГСТ ONHE, угловая скорость которого определяется выражением (4), то, очевидно, справедливы следующие выражения для их производных:

Сравнивая 1-ую и 2-ую производные с 3-ей, получим выражения:

которые, с учетом (2), можно записать в следующем виде:

Сравнивая полученные векторные выражения (7) с полученными ранее (3) и объединяя их, можно записать следующие обобщенные выражения вида:

Если представить полученные выражения в скалярном виде, в проекциях на оси географического сопровождающего трехгранника ГСТ ONHE, то они приобретут вид, вполне приемлемый для их алгоритмического использования.

Приведем его:

где , , , и , , - проекции векторов и (2) на оси ГСТ ONHE.

Полученные выражения имеют вид дифференциальных уравнений первого порядка, представленных в нормальной форме Коши, что, кстати, и необходимо для описания исходной системы - модели сообщения в традиционной процедуре оптимального оценивания. Это, если смотреть на приведенные дифференциальные уравнения слева.

С другой стороны, если на (9) и (10) смотреть справа, то это будут выражения для расчета составляющих скорости перемещения ИНС1 (9) и ИНС2 (10) относительно ДИСС.

В некоторых случаях вместо уравнений/выражений (9), (10), представленных в проекциях на оси ГСТ ONHE, целесообразно использовать аналогичные уравнения/выражения, но в проекциях на оси опорного трехгранника гироплатформы ОТГП ИНС Оξηζ.

Очевидно, что указанные уравнения/выражения, по аналогии с (9), (10) будут иметь следующий вид:

где Δξ₁, Δη₁, Δζ₁, и Δξ₂, Δη₂, Δζ₂ - текущие значения координат местоположения ИНС1/БИНС1 и ИНС2/БИНС2 относительно ДИСС в проекциях на оси ОТГП ИНС Оξηζ, a ΔV_1ξ, ΔV_lη, ΔV_1ζ и ΔV_2ξ, ΔV_2η, ΔV_2ζ - кинематические составляющие скорости движения ИНС1 и ИНС2 в проекциях на те же оси.

В процедуре оптимальной фильтрации и идентификации ошибок ИНС по измерениям ДИСС приведенные выше дифференциальные уравнения (11), (12) должны использоваться, как составная часть традиционных моделей ошибок ИНС, разработанных на основе математического описания их функционирования и в полном соответствии с основополагающим принципом невозмущенного измерения ускорений.

Включение полученных выше дифференциальных уравнений (11), (12) в проекциях на оси ОТГП ИНС Оξηζ в состав традиционной для инерциально-допплеровского режима коррекции модели ошибок ИНС позволяет получить ее расширенную модель, которая описывает не только традиционные для ИНС параметры и их связи, но и те кинематические составляющие сигналов измерения, которые ранее не учитывались.

И это обстоятельство является причиной несостоятельности существующих алгоритмов оптимального оценивания и коррекции результатов автономного инерциального счисления.

Расширение модели ошибок ИНС позволяет устранить основную причину алгоритмической несостоятельности известных алгоритмов коррекции, заключающуюся в некорректном математическом описании исходной системы, и обеспечить тем самым гарантированную наблюдаемость и устойчивую сходимость всех и, в первую очередь, слабонаблюдаемых параметров состояния, таких, как α_z, ε_y, Δn_i(Δξ_i), Δh_i(Δζ_i), Δе_i(Δη_i).

Для алгоритмического использования полученных выше дифференциальных уравнений (11), (12) необходимо знать текущие значения входных для указанных уравнений параметров, а именно, составляющих , , относительной угловой скорости вращения объекта.

Приведем возможные математические процедуры расчета рассматриваемых угловых скоростей. Для этого воспользуемся приведенной на фиг. 2, 3, 4 взаимной ориентацией ГСК OX'Y'Z', ГСТ ONHE, ОТГП ИНС Оξηζ и ССК Oxyz.

Очевидно, что угловые скорости вращения ССК Oxyz относительно ГСТ ONHE определяются угловыми скоростями , , эволюции объекта по истинному курсу, крену и тангажу. При этом угловые скорости , , и , , угловой скорости объекта относительно ГСТ ONHE и ОТГП Оξηζ могут быть определены путем приведения компонент , , и , , к осям ГСТ и ОТГП соответственно. Очевидно, они будут равны (см. фиг. 2, 3):

Здесь (13), (14) и далее под «s» следует понимать синус угла, а под «с» - косинус.

Приведенные выражения могут быть использованы для расчета искомых составляющих угловой скорости.

При этом производные , , , целесообразно определять методом численного дифференцирования с дискретом 0,1 сек.

Выражения (14), (15) могут быть использованы по их назначению как по измерениям ИНС, так и по измерениям БИНС.

На практике может быть использован и другой подход расчета рассматриваемых составляющих угловой скорости объекта, но он может быть реализован исключительно только по измерениям БИНС. Он представляется несколько более сложным, но его достоинством является отсутствие необходимости выполнения операций численного дифференцирования, что немаловажно.

Указанный вариант расчета рассматриваемых составляющих угловой скорости объекта основан на определении относительной угловой скорости и предполагает знание, как абсолютной угловой скорости вращения объекта, так и абсолютных угловых скоростей вращения ГСТ и ОТГП. При этом искомые угловые скорости находятся, как разности абсолютной угловой скорости объекта и соответственно двух вторых. По причине того, что абсолютная угловая скорость объекта измеряется исключительно только системами, типа БИНС, указанный подход может быть использован только при их коррекции.

Учитывая, что составляющие абсолютной угловой скорости объекта, измеряемые БИНС, выдаются в проекциях на оси связанной системы координат, необходимо их предварительное преобразование по осям ГСТ ONHE и ОТГП Оξηζ.

Для этого запишем прямые и обратные матричные преобразования для систем координат, приведенных на фиг. 2 и фиг. 3:

,

,

В соответствии с фиг. 2 и фиг. 3, матрицы для реализации указанных процедур, очевидно, имеют следующий вид:

В соответствии с матрицей (16) выражения для составляющих абсолютной угловой скорости объекта в проекциях на оси ГСТ ONHE будут иметь следующий вид:

Аналогичные выражения в проекциях на оси ОТГП Оξηζ, будут равны:

Для определения составляющих абсолютной угловой скорости ГСТ ONHE и ОТГП Оξηζ, введем в рассмотрение гринвическую систему координат OX'Y'Z', ось ОХ' которой ориентирована по оси мира и совпадает с угловой скоростью суточного вращения Земли, ось OZ' совпадает с линией пересечения плоскостей экватора и гринвического меридиана, а ось OY' дополняет их до правого ортогонального трехгранника. Взаимная ориентация указанной системы координат и ГСТ ONHE, ОТГП Оξηζ приведена на фиг. 4.

Все представленные на фиг. 4 углы, а именно угол географической широты ϕ, долготы λ и угол χ азимутальной ориентации опорного трехгранника гироплатформы ИНС, также, как и угловые скорости их изменения имеют положительное направление отсчета.

Для нахождения абсолютной угловой скорости ГСТ ONHE запишем выражения для угловой скорости вращения ГСТ ONHE относительно трехгранника OX'Y'Z', связанного с Землей, в проекциях на оси ГСТ ONHE. В соответствии с фиг. 4, они, очевидно, будут равны:

где приняты следующие обозначения:

где , - северная и восточная составляющие путевой скорости объекта, R_N, R_E - главные радиусы кривизны земного эллипсоида вращения

Очевидно, что искомые абсолютные составляющие угловой скорости вращения ГСТ будут равны сумме составляющих (20) и соответствующих проекций, обусловленных суточным вращением Земли, а именно:

,

где составляющие u_N и u_H равны

а u - скорость суточного вращения Земли.

Следовательно, искомые составляющие угловой скорости объекта относительно ГСТ ONHE будут равны:

где Ω_N, Ω_H, Ω_E определяются выражениями (18), a ω_N, ω_H, ω_E выржениями (22).

Для определения составляющих относительной угловой скорости ОТГП Оξηζ, в соответствии с фиг. 3, приведем все три угловые скорости , , к осям ОТГП Оξηζ. В результате получим:

Выражения для и представлены выше (21).

Очевидно, что выражения для составляющих абсолютной угловой скорости ОТГП будут равны сумме составляющих (25) и соответствующих составляющих угловой скорости суточного вращения Земли:

где u_N,u_H определяются выражениями (23).

Выражения для искомых составляющих угловой скорости вращения объекта относительно ОТГП Оξηζ будут равны:

где Ω_ξ, Ω_η, Ω_ζ определяются выражениями (19), a ω_ξ, ω_η, ω_ζ - выражениями (26).

Выше рассмотрены вопросы математически корректного описания исходной системы, которое достигается расширением традиционной для подобных систем модели ошибок путем включения в нее нетрадиционных для ИНС дифференциальных уравнений, описывающих характер изменения координат ее установки на объекте относительно той информационной системы, которая выполняет функции измерителя.

Необходимость этого расширения обусловлена тем, что только в этом случае достаточно просто и эффективно может быть обеспечен алгоритмический учет и устранение всех нежелательных последствий, к которым приводят кинематические составляющие скорости, имеющие место при маневре объекта и обусловленные геометрией относительного размещения задействованных в рассматриваемых режимах информационных систем.

При этом, предлагаемое решение следует рассматривать, как базис, на основе которого должна синтезироваться унифицированная структура оптимального фильтра-идентификатора, способного оценивать весь, расширенный перечень параметров состояния ИНС для общего случая движения объекта, включая выполнение таких маневров, как координированный и боевой развороты, «змейка», а также фигур высшего пилотажа, алгоритмических показаний к неприменению которых нет никаких.

Круг задач, при решении которых предполагается использовать предлагаемый способ, не ограничивается рассматриваемым. В частности он может быть использован и при синтезе оптимальной