Способ оптимальной привязки к подвижной наземной цели и прогноза её параметров на основе модифицированной, инвариантной к рельефу подстилающей поверхности угломестной процедуры расчёта дальности

Способ оптимальной привязки к подвижной наземной цели и прогноза её параметров на основе модифицированной, инвариантной к рельефу подстилающей поверхности угломестной процедуры расчёта дальности

Иллюстрации

Показать все

Реферат

Изобретение относится к области измерительных информационных систем и комплексов боевых самолетов и вертолетов, в которой рассматривается решение задачи привязки к подвижной наземной цели с определением ее относительного местоположения и параметров движения и их прогноза для обеспечения эффективного применения неуправляемых АСП.

Известен ряд способов решения указанной задачи, приведенных в учебнике Р.В. Мубаракшина, В.М. Балуева, Б.В. Воронова «Прицельные системы стрельбы». Часть 1, ВВИА им. Н.Е. Жуковского, 1973 г., [1]:

- способ определения скорости и ускорения цели через ее координаты и их производные (с. 43-46);

- способ определения скорости и ускорения цели путем измерения угловых скоростей и ускорений головки визирного устройства и производных дальности (с. 46-49);

- способ определения скорости и ускорения цели через ее относительные координаты, измеряемые в различные моменты времени (с. 49-51).

Перечисленные методы определения параметров движения цели представляются физически обоснованными. Но уровень их инженерной проработки и прикладная значимость не соответствуют предъявляемым к ним требованиям, а посему целесообразность их использования в современных разработках вызывает большие сомнения.

Очевидно, что при их разработке не стояла задача их промышленного использования, а преследовалась цель получения выражений для прямого расчета тех или иных параметров движения цели.

Такой подход далек от инженерного, поскольку в соответствии с ним для расчета параметров движения цели, помимо непосредственно измеряемых параметров, типа дальности до цели и углов ее визирования, предполагается использование их первых и вторых производных, что представляется недопустимым при разработке точных математических процедур.

В учебном пособии В.Г. Гришутина «Лекции по авиационным прицельным системам стрельбы». КВВАИУ, Киев, 1980 г., [2], представлен пример оптимального оценивания составляющих скорости цели только для случая ее прямолинейного и равномерного движения (с. 164-167).

Дополнительно, но уже для общего случая движения цели, в [2] в подразделе «Способ прицеливания, основанный на последовательном уточнении данных о движении цели» (см. с. 328) даются следующие рекомендации относительно определения параметров ее движения:

«В маневренном бою остро испытывается дефицит времени, поэтому при прицеливании по движущейся цели может оказаться нецелесообразным сразу точно оценивать параметры движения цели.

На практике более предпочтительной может быть их оценка, выполненная последовательно несколько раз. В каждом новом цикле оценивания производится уточнение данных, полученных в предыдущем цикле.

С каждым таким циклом точность решения рассматриваемой задачи, а следовательно, и точность прицеливания увеличиваются и достигают некоторого предельного значения, определяемого как динамикой системы оценивания, так и имеющими место случайными ошибками измерения относительных координат текущего местоположения цели».

Указанные рекомендации, если их рассматривать в пределе - при достаточно малом цикле измерения относительных координат текущего местоположения цели, не превышающем 0,1 с, и таком же цикле их обработки и оптимального оценивания по ним искомых параметров движения цели - составляющих ее скорости и ускорения, следует расценивать, как осмысленную необходимость разработки рекуррентных, сходящихся и асимптотически устойчивых, оптимальных математических процедур оценивания, нашедших применение в некоторых из отечественных разработок.

Формализуя описание основанного на приведенных рекомендациях способа привязки к подвижной наземной цели, излагая его в терминах и с акцентом на физическое содержание выполняемых при его реализации операций, приведем его в следующем виде.

Способ оптимальной привязки к подвижной наземной цели и прогноза ее параметров на основе модифицированной, инвариантной к рельефу подстилающей поверхности угломестной процедуры расчета дальности, включающий непрерывное угловое сопровождение цели и дискретное измерение дальности, по каждому из которых с использованием измеренной инерциальной навигационной системой (ИНС) угловой и навигационной информации и углов визирования цели с обзорно-прицельной системы (ОПС) формируют входные сигналы оптимального фильтра-идентификатора в виде наблюдаемых на фоне случайных шумов измерения компонент дальности до цели в проекциях на оси подвижной системы координат (ПСК), при этом оценивание параметров относительного местоположения цели и компонент ее абсолютной линейной скорости и ускорения осуществляют в соответствии с кинематической моделью относительного движения цели, структура которой определяется системой линейных взаимосвязанных дифференциальных уравнений 9-го порядка в проекциях на оси ПСК, для чего по измеренной ИНС информации осуществляют расчет составляющих абсолютной угловой скорости ПСК, а компоненты абсолютной линейной скорости объекта в проекциях на оси ПСК используют в качестве известного управления, по окончании режима привязки полученные в результате оптимальной идентификации значения оценок параметров движения цели запоминают и используют в качестве начальных условий в процедуре их прогноза, для реализации которой расчет оптимальных коэффициентов усиления останавливают, сами коэффициенты усиления и входные сигналы фильтра обнуляют, а формирование экстраполированных сигналов относительного местоположения цели и составляющих ее абсолютной линейной скорости осуществляют в соответствии с дискретной моделью относительного движения цели, при этом, как и в режиме привязки, используют рассчитанные с использованием измеренной ИНС угловой и навигационной информации текущие значения составляющих абсолютной линейной скорости объекта и компонент абсолютной угловой скорости вращения ПСК, а по текущим параметрам движения объекта и оцененным и спрогнозированным значениям параметров движения цели формируют искомые поправки на стрельбу.

Недостатками указанного способа привязки к подвижной наземной цели являются:

1. Переусложненная модель относительного движения цели, приводящая при трех измеряемых сигналах к достаточно сложной процедуре оптимального оценивания с необходимостью расчета многоразмерных [9×9] априорных и апостериорных корреляционных матриц ошибок оценивания и многоэлементной, размерностью [9×3], матрицы оптимальных коэффициентов усиления с нежелательным обращением матрицы 3-го порядка.

2. Низкая точность режима кратковременного, не превышающего 10-12 с, прогноза оцененных параметров относительного местоположения и движения цели в случае подвижной наземной цели.

Техническим результатом изобретения является:

1. Кардинальное упрощение используемой в режиме привязки к подвижной наземной цели линейной процедуры оптимальной фильтрации и идентификации параметров ее движения.

2. Повышение точности и эффективности решения боевой задачи (БЗ) за счет реализации альтернативной прогнозу параметров движения цели и унифицированной с режимом привязки математической процедуры оптимального оценивания на основе модифицированной, инвариантной к рельефу подстилающей поверхности угломестной процедуры расчета дальности.

Указанный технический результат достигается за счет того, что:

в способе оптимальной привязки к подвижной наземной цели и прогноза ее параметров на основе модифицированной, инвариантной к рельефу подстилающей поверхности угломестной процедуры расчета дальности, включающем непрерывное угловое сопровождение цели и дискретное измерение дальности, по каждому из которых с использованием измеренной инерциальной навигационной системой (ИНС) угловой и навигационной информации и углов визирования цели с обзорно-прицельной системы (ОПС) формируют входные сигналы оптимального фильтра-идентификатора в виде наблюдаемых на фоне случайных шумов измерения компонент дальности до цели в проекциях на оси подвижной системы координат (ПСК), при этом оценивание параметров относительного местоположения цели и компонент ее абсолютной линейной скорости и ускорения осуществляют в соответствии с кинематической моделью относительного движения цели, структура которой определяется системой линейных взаимосвязанных дифференциальных уравнений 9-го порядка в проекциях на оси ПСК, для чего по измеренной ИНС информации осуществляют расчет составляющих абсолютной угловой скорости ПСК, а компоненты абсолютной линейной скорости объекта в проекциях на оси ПСК используют в качестве известного управления, по окончании режима привязки полученные в результате оптимальной идентификации значения оценок параметров движения цели запоминают и используют в качестве начальных условий в процедуре их прогноза, для реализации которой расчет оптимальных коэффициентов усиления останавливают, сами коэффициенты усиления и входные сигналы фильтра обнуляют, а формирование экстраполированных сигналов относительного местоположения цели и составляющих ее абсолютной линейной скорости осуществляют в соответствии с дискретной моделью относительного движения цели, при этом, как и в режиме привязки, используют рассчитанные с использованием измеренной ИНС угловой и навигационной информации текущие значения составляющих абсолютной линейной скорости объекта и компонент абсолютной угловой скорости вращения ПСК, а по текущим параметрам движения объекта и оцененным и спрогнозированным значениям параметров движения цели формируют искомые поправки на стрельбу, дополнительно, кинематическую модель относительного движения цели представляют в проекциях на оси инерциальной системы координат, что приводит к обнулению составляющих ω_X, ω_Y, ω_Z абсолютной угловой скорости ПСК (ИСК), чем реализуют естественную поканальную декомпозицию кинематической схемы относительного движения цели, вследствие чего вместо взаимосвязанной кинематической модели 9-го порядка получают три структурно идентичных и не связанных между собой канала, на основе которых синтезируют три независимых, структурно и алгоритмически идентичных фильтра-идентификатора, каждый из которых работает на основе идентификации своей, постоянно обновляющейся последовательности компонент D_X/D_Y/D_Z дальности, которые формируют с использованием дискретно измеряемой наклонной дальности до цели , текущих углов ϕ_y, ϕ_z визирования цели, углов ψ_и, υ, γ ориентации объекта и счисленных углов географической широты ϕ и абсолютной долготы , подобную операцию, но с использованием горизонтальных сигналов абсолютной линейной скорости объекта, его вертикальной бароинерциальной скорости , угла χ текущей азимутальной ориентации гироплатформы (ГП) ИНС и счисленных значений географической широты ϕ и абсолютной долготы , осуществляют и при расчете составляющих абсолютной линейной скорости объекта, которые используют в процедуре оптимальной фильтрации и идентификации в качестве известного управления, дополнительно, параллельно с процедурой оптимальной фильтрации и идентификации параметров относительного местоположения и движения цели, выполняют ряд вспомогательных операций для реализации точного, инвариантного по отношению к рельефу подстилающей поверхности, модифицированного угломестного способа определения наклонной дальности и на его основе унифицированной с режимом привязки процедуры оптимального оценивания, для чего, используя каждое измеренное значение дальности , формируют текущее значение косинуса сθ_i угла между географической вертикалью и линией визирования цели и определяют текущее значение высоты h_i объекта над уровнем движения цели, после чего указанное значение высоты h_i сравнивают с текущей высотой объекта над уровнем моря , сформированной в результате оптимального комплексирования вертикального канала ИНС и баровысотомера системы воздушных сигналов (СВС), а получаемые в результате сравнения значения высоты цели Δh_i над уровнем моря осредняют на интервале привязки к цели, используя рекуррентную процедуру нахождения среднего, и получают среднее на интервале привязки значение , по окончании которой, не прерывая процедуры аппаратного углового сопровождения подвижной цели, на каждом такте решения указанной задачи формируют расчетные значения текущей высоты объекта над целью и косинус cθ_i, по которым определяют модифицированную угломестную дальность , и так же, как и в режиме привязки, формируют значения компонент D_X/D_Y/D_Z дальности и используют их в качестве сигналов измерения в унифицированной с режимом привязки процедуре оптимального оценивания, которую реализуют как альтернативу режиму прогноза параметров движения цели.

Приведем перечень и описание чертежей, которые потребуются при осуществлении предлагаемого изобретения.

На фиг. 1 приведена произвольная ориентация подвижной Oxyz и неподвижной OXYZ систем координат.

В общем случае, в качестве подвижной системы координат могут быть приняты:

- связанная с объектом система координат (ССК) Oxyz;

- лучевая система координат (ЛСК) , продольная ось Ох_Л которой ориентирована в направлении цели;

- географический сопровождающий трехгранник (ГСТ) ONHE;

- гринвичская система координат (ГСК) .

В качестве подвижной может быть использована и абсолютно неподвижная - инерциальная система координат (ИСК) OXYZ.

Далее будем считать, что положение подвижной системы координат относительно неподвижной - ИСК OXYZ, определяется радиусом-вектором , а положение цели (Ц) относительно ИСК OXYZ - радиусом-вектором , при этом положение цели относительно подвижной системы координат определяется вектором дальности (см. фиг. 1).

На фиг. 1 также обозначено:

- абсолютная линейная скорость объекта; - абсолютная линейная скорость цели. Под термином «абсолютная» следует понимать скорость относительно инерциального пространства - ИСК.

На фиг. 2 приведена ориентация ИСК OXYZ, ГСК и ГСТ ONHE на земном эллипсоиде вращения. ГСК - это система координат, связанная с Землей, ось ОХ’ которой параллельна оси вращения Земли, ось OZ’ лежит в плоскости гринвичского меридиана, а ось OY' дополняет их до правого ортогонального трехгранника и направлена на запад.

ИСК OXYZ - это абсолютно неподвижная система координат, связанная со звездами. Рассогласование ГСК и ИСК OXYZ определяется углом ut, где u - угловая скорость суточного вращения Земли, t - текущее время (фиг. 2).

На фиг. 3 приведена взаимная ориентация ГСК и ГСТ ONHE.

Их рассогласование определяется углами географической долготы λ и широты ϕ.

Переход от осей ГСК к осям ГСТ ONHE осуществляется посредством двух последовательных поворотов на угол λ и угол ϕ с угловыми скоростями и соответственно.

Приведенное на фиг. 3 направление отсчета углов λ и ϕ и угловых скоростей и является положительным.

На фиг. 4 приведена взаимная ориентация ССК Oxyz и ЛСК .

Их рассогласование определяется углами ϕ_y, ϕ_z визирования цели. Ось Ох_Л ЛСК направлена на цель, с указанной осью при угловом сопровождении цели совпадает вектор наклонной дальности до цели (фиг. 1).

Переход от осей ССК Oxyz к осям ЛСК осуществляется посредством двух последовательных поворотов на углы ϕ_y и ϕ_z с угловыми скоростями и соответственно.

Приведенное на фиг. 4 направление отсчета углов ϕ_y, ϕ_z и угловых скоростей , является положительным.

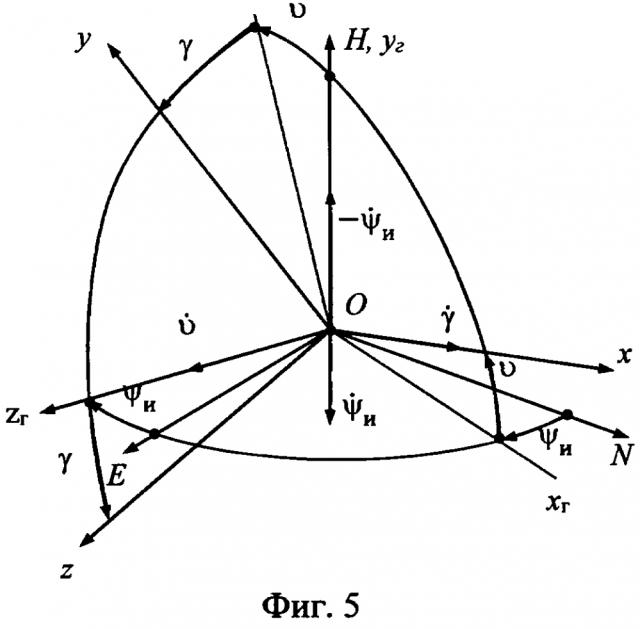
На фиг. 5 приведена взаимная ориентация ГСТ ONHE и ССК Oxyz.

Их рассогласование определяется углами истинного курса ψ_и, тангажа υ и крена γ объекта.

Переход от осей ГСТ ONHE к осям ССК Oxyz осуществляется посредством трех последовательных поворотов на углы ψ_и, υ и γ с угловыми скоростями и .

Приведенное на фиг. 5 направление отсчета углов ψ_и, υ, γ и угловых скоростей является положительным.

На фиг. 6 приведена возможная схема относительного движения цели (Ц) для случая полета объекта (ЛА) над холмисто-гористой подстилающей поверхностью.

Под приведенными на указанной схеме обозначениями параметров движения объекта и цели следует понимать:

- измеренное лазерным дальномером i-е значение дальности до цели;

θ_i - угол между местной географической вертикалью и направлением на цель, косинус сθ_i угла которого сформирован по i-м измерениям углов визирования цели и углов крена и тангажа объекта;

УМ - уровень моря, относительно которого осуществляется отсчет бароинерциальной высоты , сформированной как результат оптимального комплексирования измерений вертикального канала ИНС и баровысотомера из состава системы воздушных сигналов (СВС);

h_i - расчетное значение текущей i-й высоты объекта относительно цели, или иначе, превышение объекта над целью, расчет h_i осуществляют в соответствии с выражением ,

Δh_i - текущее i-е значение высоты цели над уровнем моря, формируется сравнением бароинерциальной высоты и расчетной высоты h_i объекта:

- векторы абсолютной линейной скорости объекта и цели соответственно.

С целью раскрытия физической и математической сути предлагаемого способа приведем подробное описание используемых при этом систем координат, матричных преобразований, дифференциальных уравнений относительного движения объекта и цели и входящих в них параметров, а также оптимальных математических процедур дискретной фильтрации Калмана.

В соответствии со взаимной ориентацией подвижной Oxyz и неподвижной (инерциальной) OXYZ систем координат и векторов, определяющих относительное местоположение объекта и цели (фиг. 1), и известной леммой о нахождении абсолютной производной некоторого вектора, приведенной в «Курсе теоретической механики» Л.Г. Лойцянского и А.И. Лурье. Том 1. Москва, «Наука», 1982 г. [3] (с. 302), можно достаточно просто показать, что векторное дифференциальное уравнение относительного движения цели имеет вид:

где - вектор дальности между объектом и целью; и - векторы абсолютной линейной скорости цели и объекта соответственно; - вектор абсолютной угловой скорости вращения подвижной системы координат Oxyz; - символ локальной производной.

При скалярном представлении векторного уравнения (1) необходимо помнить, что оно должно быть записано в проекциях на оси подвижной системы координат Oxyz:

Приведенной системой дифференциальных уравнений описывается относительное движение объекта и цели в самом общем случае. Указанную структуру будут иметь дифференциальные уравнения в проекциях на оси географического сопровождающего трехгранника ГСТ ONHE и связанной с вертолетом систем координат ССК Oxyz.

Из этого ряда выпадают дифференциальные уравнения в проекциях на оси лучевой ЛСК и гринвичской ГСК систем координат. Особое место в этом ряду занимает случай, когда в качестве подвижной принимается инерциальная система отсчета ИСК OXYZ.

Принципиальным отличием этого варианта от всех предыдущих является то, что абсолютная угловая скорость подвижной (инерциальной) системы координат относительно неподвижной (инерциальной) системы координат будет равна нулю, т.е. ω_X=ω_Y=ω_Z=0, что приводит к закономерному упрощению представленной выше системы дифференциальных уравнений (2), которая в рассматриваемом случае примет вид:

Впервые на указанное свойство ИСК OXYZ применительно к модели относительного движения цели обратили внимание в [1] (с. 49, 5-9-я строки сверху).

Из приведенной системы дифференциальных уравнений (3) следует, что для рассматриваемого случая взаимосвязанная система уравнений (2) трансформируется в систему трех независимо интегрируемых уравнений первого порядка, что позволит не только упростить процедуру их численного интегрирования, но и синтезировать на их основе достаточно эффективные и математически строгие алгоритмы привязки к цели и ее программного сопровождения. При этом и процедура привязки к цели (с определением параметров ее движения), и ее программного сопровождения - прогноза, являются краткосрочными и, в общем случае, не превышают 13-15 с, из которых 3 с приходятся на режим привязки.

Для осуществления возможных преобразований и пересчетов произвольных векторов, заданных в проекциях на оси лучевой системы координат или географического сопровождающего трехгранника ГСТ к осям гринвичской системы координат ГСК и далее, к инерциальной системе отсчета ИСК и обратно, воспользуемся приведенной на фиг. 3, 4, 5 взаимной ориентацией введенных в рассмотрение систем координат.

В соответствии с фиг. 3, матричные преобразования произвольного вектора из гринвичской системы координат OX’Y’Z’ к осям ГСТ ONHE и обратно имеют вид:

где матрицы G и G^T будут равны:

В выражениях (5) и далее под «s» следует понимать синус угла, а под «с» - косинус.

Матричные преобразования произвольного вектора из ГСТ ONHE в ССК Oxyz и обратно имеют вид:

где матрица S_Г и транспонированная ей матрица , в соответствии с фиг. 4, равны:

Матричные преобразования произвольного вектора из ССК Oxyz в ЛСК и обратно имеют вид:

Входящие в (8) матрицы L и , в соответствии с фиг. 5, равны:

Таким образом, согласно (4), (6) и (8), преобразование произвольного вектора, заданного в осях ЛСК, к осям гринвичской системы координат ГСК OX'Y'Z' может быть осуществлено в соответствии со следующим матричным выражением:

где матрица получается перемножением соответствующих матриц (5), (7) и (9).

Для преобразования произвольного вектора, заданного проекциями на оси лучевой системы координат, под которым следует понимать измеренный лазерным дальномером массив наклонной дальности, к осям инерциальной системы отсчета воспользуемся полученным выше матричным соотношением (4), в котором под матрицей G^T (5) будем понимать аналогичную по структуре матрицу с той лишь разницей, что в ней вместо географической долготы λ, отсчитываемой от плоскости гринвичского меридиана, будем использовать абсолютную долготу , равную:

где u - угловая скорость суточного вращения Земли.

В соответствии с представленной на фиг. 3 ориентацией осей инерциальной OXYZ и гринвичской OX’Y’Z’ систем координат, отсчет осуществляется относительно оси OZ.

При этом при расчете текущего времени t_k отсчет времени будем вести от начала режима привязки, а его расчет осуществлять в соответствии со следующим рекуррентным выражением:

t_k=t_k-1+τ,

где τ - дискрет счета, который для рассматриваемой задачи равен 0,1 с, t₀=0.

В дальнейшем, описанную выше матрицу, с использованием которой осуществляют преобразование компонент произвольного вектора от осей ГСТ ONHE к осям ИСК OXYZ, будем обозначать , а обратную ей - .

Очевидно, что использование указанных матриц в векторно-матричном преобразовании (10) и обратном ему позволит реализовать следующие полезные преобразования компонент произвольного вектора:

Для формирования полной модели относительного движения цели дополним дифференциальные уравнения (3) уравнениями, описывающими характер изменения скорости цели для случая ее движения с постоянным ускорением. В соответствии с теоремой Кориолиса, устанавливающей порядок определения абсолютной производной в подвижной системе координат, указанные уравнения будут иметь следующий вид:

Объединяя (3) и (13), получим полную модель относительного движения цели, представленную в проекциях на оси ИСК:

Из представленных уравнений следует, что в рассматриваемом случае, когда подвижная и неподвижная системы координат совпадают, модель относительного движения объекта и цели представляет собой поканально несвязанную модель, включающую три самостоятельных канала X (14), Y (15), Z(16).

Уравнения (14), (15), (16) будут использованы при разработке алгоритма идентификации скорости и ускорения движения цели, потому как разработанные на их основе математические процедуры привязки к цели и программного сопровождения будет отличать высокая степень унификации, простота алгоритмической и программной реализации, высокое быстродействие и точность.

При этом преобразование составляющих абсолютной линейной скорости объекта, заданных в проекциях на оси ГСТ ONHE, к инерциальным осям осуществляют в соответствии с описанным выше матричным соотношением вида:

а обратное преобразование оценок скорости цели, в соответствии с матричным соотношением:

где матрица и обратная ей матрица представлены выше и имеют структуру, аналогичную (5), с той лишь разницей, что в них используется абсолютная долгота (11).

Синтез структуры оптимального идентификатора будем проводить в соответствии с традиционной линейной процедурой оптимальной фильтрации Калмана. Приведем сводку ее основных соотношений, представленную в Э. Сейдж, Дж. Мелс «Теория оценивания и ее применение в связи и управлении», «Связь», Москва, 1976, [4] (см. с. 269).

1. Исходная модель сообщения:

2. Модель наблюдения:

3. Априорные данные, используемые при синтезе:

4. Структура оптимального фильтра:

где

5. Вычисление оптимальных коэффициентов усиления:

6. Вычисление матрицы априорных ошибок оценивания:

7. Вычисление матрицы апостериорных ошибок оценивания:

В приведенных выше соотношениях приняты следующие условные обозначения:

x_k - вектор параметров состояния системы;

- вектор оптимальных апостериорных оценок параметров состояния;

w_k - вектор случайных возмущений модели сообщения;

V_k - вектор случайных шумов измерения;

Ф_k+1,k - фундаментальная матрица системы (модели сообщения);

Г_k+1,k - матрица передачи случайных возмущений системы;

H_k - матрица измерения;

- вектор априорных оценок параметров состояния системы;

P_k+1,k - априорная корреляционная матрица ошибок оценивания;

P_k+1 - апостериорная корреляционная матрица ошибок оценивания;

Q_k - корреляционная матрица случайных шумов системы;

R_k - корреляционная матрица случайных шумов измерения;

z_k - вектор сигналов измерения;

K_k+1 - матрица оптимальных коэффициентов усиления.

В соответствии с системой дифференциальных уравнений (14), (15), (16), модель сообщения исследуемой системы будет иметь следующий вид:

1. Канал X

2. Канал Y

3. Канал Z

где - белые шумы возмущений, действующих в каждом из каналов;

τ - дискретность вычислений.

В соответствии с (26) фундаментальные матрицы для каналов X, Y и Z будут иметь вид:

Матрицы передачи случайных возмущений w_Xik, w_Yik, w_Zik, очевидно, будут равны:

Корреляционные матрицы Q_X, Q_Y, Q_Z возмущающих шумов модели сообщения представим в следующем виде:

где - дисперсии возмущающих шумов по дальности, скорости и ускорению соответственно.

Так как измеряемыми параметрами являются составляющие D_Xk+1, D_Yk+1, D_Zk+1 дальности до цели в проекциях на оси инерциальной системы координат OXYZ, то сигналы измерения для каждого из каналов могут быть представлены в виде:

где V_Xk+1, V_Yk+1, V_Zk+1 - некоррелированные гауссовские шумы сигналов измерения.

Матрицы измерения H_X, H_Y, H_Z, учитывая, что векторы параметров состояния для каждого из каналов имеют вид:

будут равны:

Корреляционные матрицы шумов измерения равны:

где σ² - дисперсия измерительных шумов в тракте измерения дальности.

Матрицы оптимальных коэффициентов усиления для каждого из рассматриваемых каналов будут иметь вид:

Процедура расчета указанных матриц является традиционной и осуществляется в соответствии с матричным выражением (23).

В соответствии с (14), (15), (16) и (22), выражения для расчета апостериорных оценок будут иметь вид:

В приведенных уравнениях компоненты с индексами k+1,k - априорные оценки соответствующих параметров состояния системы (см. матричные выражения (22)). Выражения для их расчета равны:

Представленные в дискретном виде уравнения для расчета априорных оценок (38), (39), (40), использующиеся в общей процедуре оптимального оценивания (35), (36), (37) в режиме привязки к цели, могут быть использованы и в режиме прогноза параметров относительного движения цели, который должен быть реализован на основе полученных в привязке оценок.

Дополнительно, в качестве альтернативного варианта алгоритмической реализации экстраполяции параметров подвижной наземной цели может быть предложена процедура, основанная на модифицированном угломестном методе расчета текущей дальности до цели и последующем использовании постоянно обновляющегося массива сигналов измерения Z_X, Z_Y, Z_Z (30) оптимальных фильтров-идентификаторов (35), (36), (37), разработанных в соответствии с полученной выше моделью относительного движения цели, представленной дифференциальными уравнениями (14), (15), (16).

Достоинством такого алгоритмического решения является использование как на первом, активном этапе привязки к цели с измерением дальности, так и на втором этапе углового сопровождения цели одной и той же математической процедуры оптимального оценивания, вторая из которых основана на модифицированной процедуре угломестного метода определения текущей дальности до движущейся наземной цели.

Суть модификации заключается в том, что на первом этапе активной фазы привязки к цели для каждого измеренного лазерным дальномером ЛД значения дальности D_i определяют значение высоты h_i, при которой виртуальная угломестная дальность до цели была бы равна измеренной ЛД дальности D_i. Формула для расчета указанной высоты h_i имеет вид:

где cθ_i определяется выражением:

В приведенных выражениях под i следует понимать номер произведенных измерений дальности D_i, углов ϕ_yi, ϕ_zi, υ_i, γ_i и расчета виртуальной высоты h_i