Способ оптимальной привязки к подвижной наземной цели и прогноза её параметров на основе субоптимальной процедуры углового сопровождения

Способ оптимальной привязки к подвижной наземной цели и прогноза её параметров на основе субоптимальной процедуры углового сопровождения

Иллюстрации

Показать все

Реферат

Изобретение относится к области измерительных информационных систем и комплексов боевых самолетов и вертолетов, в котором рассматривается решение одной из задач прицеливания, заключающейся в разработке точной процедуры привязки к подвижной наземной цели с определением ее текущего относительного местоположения и параметров движения, и их прогноза в обеспечение эффективного применения неуправляемых авиационных средств поражения (АСП).

Известен ряд способов определения параметров движения цели, приведенных в учебнике Р.В. Мубаракшина, В.М. Балуева, Б.В. Воронова «Прицельные системы стрельбы», часть 1, ВВИА им. Н.Е. Жуковского, 1973 г., [1].

Приведем их:

- способ определения скорости и ускорения цели через ее координаты и их производные (стр. 43-46);

- способ определения скорости и ускорения цели путем измерения угловых скоростей и ускорений головки визирного устройства и производных дальности (стр. 46-49);

- способ определения скорости и ускорения цели через ее относительные координаты, измеряемые в различные моменты времени (стр. 49-51).

Перечисленные методы определения параметров движения цели представляются физически обоснованными. Но при этом уровень их инженерной проработки и прикладная значимость не соответствуют предъявляемым к ним требованиям, а посему целесообразность их использования в современных разработках вызывает большие сомнения.

И причина этого в том, что при их разработке, очевидно, не стояла задача синтеза рекуррентных, сходящихся и асимптотически устойчивых оптимальных математических процедур оценивания искомых параметров движения цели, а преследовалась цель получения выражений для прямого расчета тех или иных параметров движения цели.

Такой подход очень далек от инженерного, поскольку, в соответствии с ним, для расчета параметров движения цели, помимо непосредственно измеряемых параметров, типа дальности до цели и углов ее визирования, предполагается использование их первых и вторых производных, что представляется недопустимым при разработке точных математических процедур.

В учебном пособии В.Г. Гришутина «Лекции по авиационным прицельным системам стрельбы», КВВАИУ, Киев, 1980 г., [2] представлен пример оптимального оценивания составляющих скорости цели для случая ее прямолинейного и равномерного движения (см. стр. 164-167).

Упрощенная модель движения цели, не предполагающая выполнения даже самых элементарных маневров и используемая при его разработке непрерывная процедура оптимальной фильтрации Калмана, которая, как показывает опыт ее применения, может быть использована только для синтеза структуры фильтра, что является малой частью решения поставленной задачи, не позволяет принять рассматриваемый пример в качестве прототипа.

Дополнительно, но уже для общего случая движения цели, в [2], в подразделе «Способ прицеливания, основанный на последовательном уточнении данных о движении цели» (см. стр. 328) даются следующие рекомендации относительно определения параметров ее движения:

«В маневренном бою остро испытывается дефицит времени, поэтому при прицеливании по движущейся цели может оказаться нецелесообразным сразу точно оценивать параметры движения цели.

На практике более предпочтительной может быть их оценка, выполненная последовательно несколько раз. В каждом новом цикле оценивания производится уточнение данных, полученных в предыдущем цикле.

С каждым таким циклом точность решения рассматриваемой задачи, а, следовательно, и точность прицеливания, увеличивается и достигает некоторого предельного значения, определяемого, как динамикой системы оценивания, так и имеющими место случайными ошибками измерения относительных координат текущего местоположения цели».

Указанные рекомендации, если их рассматривать в пределе - при достаточно малом цикле измерения относительных координат текущего местоположения цели, не превышающем 0,1 секунды, и таком же цикле их обработки и оптимального оценивания по ним искомых параметров движения цели - составляющих ее скорости и ускорения, следует расценивать, как осмысленную необходимость разработки рекуррентных, сходящихся и асимптотически устойчивых, оптимальных математических процедур оценивания, нашедших применение в некоторых из отечественных разработок.

Формализуя описание основанного на приведенных рекомендациях способа привязки к подвижной наземной цели, излагая его в терминах и с акцентом на физическое содержание выполняемых при его реализации операций, приведем его в следующем виде.

Способ оптимальной привязки к подвижной наземной цели и прогноза ее параметров на основе субоптимальной процедуры углового сопровождения, включающий реализацию процедуры ее непрерывного углового сопровождения и ограниченного во времени, не превышающего 3-х секунд, дискретного измерения наклонной дальности до нее, по каждому из которых с использованием измеряемой инерциальной навигационной системой (ИНС) угловой и навигационной информации и текущих углов ϕ_y, ϕ_z визирования цели с обзорно-прицельной системы (ОПС) формируют входные сигналы оптимального фильтра-идентификатора в виде наблюдаемых на фоне случайных шумов измерения компонент дальности до цели в проекциях на оси подвижной системы координат (ПСК), при этом оценивание параметров относительного местоположения цели и компонент ее абсолютной линейной скорости и ускорения осуществляют в соответствии с кинематической моделью относительного движения цели, структура которой определяется системой линейных взаимосвязанных дифференциальных уравнений 9-го порядка в проекциях на оси ПСК, для чего по измеренной ИНС информации осуществляют расчет составляющих абсолютной угловой скорости ПСК, а компоненты абсолютной линейной скорости объекта используют в качестве известного управления, по окончании режима привязки полученные в результате оптимальной идентификации значения оценок параметров движения цели запоминают и используют в качестве начальных условий в процедуре их прогноза, для реализации которой расчет оптимальных коэффициентов усиления останавливают, сами коэффициенты усиления и входные сигналы фильтра обнуляют, а формирование экстраполированных сигналов относительного местоположения цели и составляющих ее абсолютной линейной скорости осуществляют в соответствии с дискретной схемой относительного движения цели, при этом, как и в режиме привязки, используют рассчитанные с использованием навигационной информации текущие значения составляющих абсолютной линейной скорости объекта и компонент абсолютной угловой скорости вращения ПСК, а по текущим параметрам движения объекта и оцененным и спрогнозированным значениям параметров движения цели формируют искомые поправки на стрельбу.

Приведенный способ оптимальной привязки к подвижной наземной цели и прогноза ее параметров по своей технической сути может быть принят в качестве наиболее близкого аналога.

Недостатком указанного способа является отсутствие возможности организации корректной субоптимальной процедуры оценивания параметров движения цели в режиме ее пассивного - без измерения дальности, углового сопровождения и, как следствие, низкая точность режима кратковременной, не превышающей 10-12-ти секунд, экстраполяции параметров движения, в общем случае, маневрирующей наземной цели.

Техническим результатом изобретения является расширение функциональных возможностей режима привязки к подвижной наземной цели и повышение точности оптимального оценивания и краткосрочного прогноза ее параметров на основе субоптимальной процедуры углового сопровождения.

Указанный технический результат достигается за счет того, что в способе оптимальной привязки к подвижной наземной цели и прогноза ее параметров на основе субоптимальной процедуры ее углового сопрвождения, включающем реализацию процедуры непрерывного углового сопровождения и ограниченного во времени, не превышающего 3-х секунд, дискретного измерения наклонной дальности до нее, по каждому из которых с использованием измеряемой инерциальной навигационной системой (ИНС) угловой и навигационной информации и текущих углов ϕ_y, ϕ_z визирования цели с ОПС формируют входные сигналы оптимального фильтра-идентификатора в виде наблюдаемых на фоне случайных шумов измерения компонент дальности до цели в проекциях на оси подвижной системы координат (ПСК), при этом оценивание параметров относительного местоположения цели и компонент ее абсолютной линейной скорости и ускорения осуществляют в соответствии с кинематической моделью относительного движения цели, структура которой определяется системой линейных взаимосвязанных дифференциальных уравнений 9-го порядка в проекциях на оси ПСК, для чего по измеренной ИНС информации осуществляют расчет составляющих абсолютной угловой скорости ПСК, а компоненты абсолютной линейной скорости объекта в проекциях на оси ПСК используют в качестве известного управления, по окончании режима привязки полученные в результате оптимальной идентификации значения оценок параметров движения цели запоминают и используют в качестве начальных условий в процедуре их прогноза, для реализации которой расчет оптимальных коэффициентов усиления останавливают, сами коэффициенты усиления и входные сигналы фильтра обнуляют, а формирование экстраполированных сигналов относительного местоположения цели и составляющих ее абсолютной линейной скорости осуществляют в соответствии с дискретной моделью относительного движения цели, при этом, как и в режиме привязки, используют рассчитанные с использованием навигационной информации текущие значения составляющих абсолютной линейной скорости объекта и компонент абсолютной угловой скорости вращения ПСК, а по текущим параметрам движения объекта и оцененным и спрогнозированным значениям параметров движения цели формируют искомые поправки на стрельбу, дополнительно, в качестве подвижной используют систему координат, связанную с линией визирования (ЛВ) цели, а в качестве входных сигналов оптимального фильтра-идентификатора - измеряемые обзорно-прицельной системой текущие значения наклонной дальности D_Л и углов ϕ_y, ϕ_z визирования цели, посредством оптимальной фильтрации и идентификации которых оценивают полный перечень параметров относительного местоположения и движения цели, при этом по измерениям угловой и навигационной информации ИНС и углов визирования цели рассчитывают текущие значения составляющих абсолютной угловой скорости связанной (ССК) Oxyz и лучевой (ЛСК) систем координат в проекциях на оси ЛСК, а также, используемые в качестве известных сигналов управления - компоненты абсолютной линейной скорости движения объекта в осях ЛСК, по окончании режима привязки, полученные значения оценок запоминают, a оптимальный фильтр-идентификатор параметров движения цели редуцируют, для чего из него выделяют параметры дальномерного канала, а на основе редуцированной модели углового сопровождения цели, описывающей характер изменения параметров ϕ_y, ϕ_z, , не прерывая ее физического углового сопровождения, реализуют субоптимальную процедуру их оценивания по измерениям текущих углов ϕ_y, ϕ_z визирования цели, параллельно с которой организуют программный прогноз параметров дальномерного канала, при этом, на 1-ом такте прогноза используют запомненные на момент окончания режима привязки к цели значения оценок , текущие значения составляющих абсолютной угловой скорости ЛСК и компоненты абсолютной линейной скорости объекта, а на 2-ом и последующих тактах - спрогнозированные значения и оцененные редуцированным фильтром значения составляющих скорости цели, а в качестве составляющих абсолютной угловой скорости ЛСК и компоненты абсолютной линейной скорости объекта - текущие расчетные значения указанных параметров, при этом, при субоптимальном оценивании в режиме углового сопровождения цели, в качестве начальных значений оценок используют запомненные на момент окончания привязки значения соответствующих параметров, а в качестве параметров дальномерного канала - спрогнозированные значения его параметров .

Приведем перечень и описание фигур, которые потребуются при осуществлении предлагаемого изобретения.

На фиг. 1 приведена произвольная ориентация подвижной Oxyz и неподвижной OXYZ систем координат.

В общем случае, в качестве подвижной системы координат могут быть приняты:

- связанная с объектом система координат (ССК) Oxyz;

- лучевая система координат (ЛСК) , продольная ось Ох_Л которой ориентирована в направлении цели;

- географический сопровождающий трехгранник (ГСТ) ONHE;

- гринвическая система координат (ГСК) .

В качестве подвижной может быть использована и абсолютно неподвижная - инерциальная система координат (ИСК) OXYZ.

Далее будем считать, что положение подвижной системы координат относительно неподвижной - ИСК OXYZ определяется радиусом-вектором , а положение цели (Ц) относительно ИСК OXYZ - радиусом-вектором , при этом положение цели относительно подвижной системы координат определяется вектором (см. фиг. 1).

На фиг. 1 также обозначено:

- абсолютная линейная скорость объекта; - абсолютная линейная скорость цели. Под термином «абсолютная» следует понимать скорость относительно инерциального пространства - ИСК.

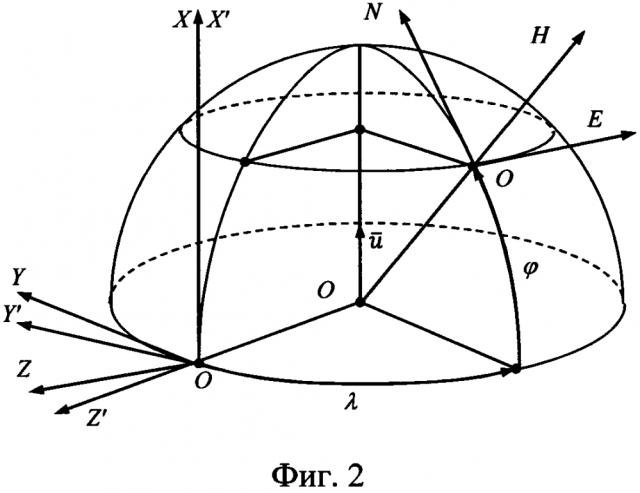
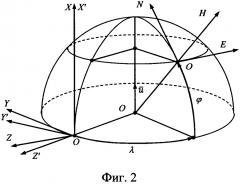
На фиг. 2 приведена ориентация ИСК OXYZ, ГСК и ГСТ ONHE на земном эллипсоиде вращения. ГСК - это система координат, связанная с Землей, ось ОХ’ которой параллельна оси вращения Земли, ось OZ’ - лежит в плоскости гринвического меридиана, а ось OY’ дополняет их до правого ортогонального трехгранника и направлена на Запад.

ИСК OXYZ - это абсолютно неподвижная система координат, связанная со звездами. Рассогласование ГСК и ИСК OXYZ определяется углом ut, где u - угловая скорость суточного вращения Земли, t - текущее время (см. фиг. 2).

На фиг. 3 приведена взаимная ориентация ГСК и ГСТ ONHE.

Их рассогласование определяется углами географической долготы λ и широты ϕ.

Переход от осей ГСК к осям ГСТ ONHE осуществляется посредством двух последовательных поворотов на угол λ, и угол ϕ с угловыми скоростями и соответственно.

Приведенное на фиг. 3 направление отсчета углов λ и ϕ и угловых скоростей и является положительным.

На фиг. 4 приведена взаимная ориентация ССК Oxyz и ЛСК .

Их рассогласование определяется углами ϕ_y, ϕ_z визирования цели. Ось Ох_Л ЛСК направлена на цель, с указанной осью при угловом сопровождении цели совпадает вектор наклонной дальности до цели (см. фиг. 1).

Переход от осей ССК Oxyz к осям ЛСК осуществляется посредством двух последовательных поворотов на углы ϕ_y и ϕ_z с угловыми скоростями и соответственно.

Приведенное на фиг. 4 направление отсчета углов ϕ_y, ϕ_z и угловых скоростей является положительным.

На фиг. 5 приведена взаимная ориентация ГСТ ONHE и ССК Oxyz.

Их рассогласование определяется углами истинного курса ψ_и, тангажа υ и крена γ объекта.

Переход от осей ГСТ ONHE к осям ССК Oxyz осуществляется посредством трех последовательных поворотов на углы ψ_и, υ и γ с угловыми скоростями и .

Приведенное на фиг. 5 направление отсчета углов ψ_и, υ, γ и угловых скоростей является положительным.

С целью раскрытия физической сути и математического содержания предлагаемого способа приведем подробное описание используемых при этом векторно-матричных преобразований, дифференциальных уравнений относительного движения объекта и цели и входящих в них параметров, а также оптимальных математических процедур дискретной фильтрации и идентификации Калмана.

В соответствии со взаимной ориентацией подвижной Oxyz и неподвижной (инерциальной) OXYZ систем координат и векторов, определяющих относительное местоположение объекта и цели (фиг. 1), и известной леммой о нахождении абсолютной производной некоторого вектора, приведенной в «Курсе теоретической механики» Л.Г. Лойцянского и А.И. Лурье, Том 1, Москва, «Наука», 1982 г [3] (стр. 302) можно достаточно просто показать, что векторное дифференциальное уравнение относительного движения цели имеет вид:

где - вектор дальности между объектом и целью; и - векторы абсолютной линейной скорости цели и объекта соответственно; - вектор абсолютной угловой скорости вращения подвижной системы координат Oxyz; - символ локальной производной.

При скалярном представлении векторного уравнения (1) необходимо помнить, что оно должно быть записано в проекциях на оси подвижной системы координат Oxyz:

Приведенной системой дифференциальных уравнений описывается относительное движение объекта и цели в самом общем случае. Указанную структуру будут иметь дифференциальные уравнения в проекциях на оси географического сопровождающего трехгранника ГСТ ONHE и связанной с объектом систем координат ССК Oxyz.

Для записи указанных уравнений в проекциях на оси лучевой системы координат ЛСК , необходимо помнить, что, по определению, ось Ох_Л ЛСК ориентирована в направлении цели и совпадает с вектором дальности , а поэтому для нее справедливо:

Подставляя (3) в уравнения (2), получим:

Полученные выражения являются искомыми для лучевой системы координат ЛСК. Из них следует, что для ЛСК взаимосвязанная система уравнений вида (2) трансформируется в обыкновенное дифференциальное уравнение первого порядка для наклонной дальности и в два выражения для составляющих абсолютной угловой скорости линии визирования обзорно-прицельной системы ОПС.

Для получения выражений для расчета составляющих абсолютной угловой скорости вращения ЛСК в проекциях на ее же оси воспользуемся приведенной на фигурах 3, 4, 5 взаимной ориентацией введенных в рассмотрение систем координат.

В соответствии с фиг. 3, матричные преобразования произвольного вектора из ГСК в ГСТ ONHE и обратно имеют вид:

где матрицы G и G^T будут равны:

В выражениях (6) и далее под «s» следует понимать синус угла, а под «с» - косинус.

Матричные преобразования произвольного вектора из ГСТ ONHE в ССК Oxyz и обратно, в соответствии с фиг. 4, имеют вид:

Матрицы S_Г и транспонированная ей матрица в соответствии с фиг. 4 имеют вид:

Матричные преобразования произвольного вектора из ССК Oxyz в ЛСК и обратно имеют вид:

Входящие в (9) матрицы L и L^T, в соответствии с фиг. 5, имеют вид:

Приведем необходимые при дальнейшем рассмотрении математические процедуры для расчета составляющих абсолютной угловой скорости ЛСК в проекциях на ее же оси, используя которые, на основе полученной выше системы (4), разработаем искомое математическое описание кинематической модели относительного движения системы «объект-цель» применительно к реализации оптимальной процедуры привязки к подвижной наземной цели с определением текущих координат ее относительного местоположения и параметров движения в проекциях на оси ЛСК и их последующей экстраполяции.

Самой простой из них является процедура, предполагающая использование измерений БИНС, в перечень выходных сигналов которых входят составляющие Ω_x, Ω_y, Ω_z абсолютной угловой скорости объекта в проекциях на связанные с ним оси.

Очевидно, что проектируя составляющие Ω_x, Ω_y, Ω_z на оси ЛСК Оx_лy_лz_л и суммируя полученные компоненты с соответствующими составляющими , относительной угловой скорости ЛСК Оx_лy_лz_л (фиг. 4):

получим искомые составляющие абсолютной угловой скорости.

Приведем их:

В варианте с ИНС платформенного типа указанная процедура существенно усложняется и осуществляется в несколько этапов. Приведем ее.

На первом этапе рассчитывают составляющие абсолютной угловой скорости ГСТ ONHE в проекциях на его же оси, которые, в соответствии с фиг. 3, очевидно, будут равны:

где u - угловая скорость суточного вращения Земли, а выражения для расчета и имеют вид:

В последних выражениях R_N и R_E - главные радиусы кривизны земного эллипсоида вращения. После чего указанные составляющие угловой скорости приводят к осям связанной системы координат Oxyz. Выражения, в соответствии с которыми осуществляется эта операция, имеют вид:

Выражения для расчета составляющих угловой скорости вращения объекта относительно ГСТ ONHE, в соответствии с фиг. 5, имеют вид:

Суммируя соответствующие составляющие угловых скоростей и (i=x, y, z) получим выражения для расчета составляющих Ω_x, Ω_y, Ω_z абсолютной угловой скорости связанной с объектом системы координат:

Последняя операция по расчету составляющих абсолютной угловой скорости ЛСК в проекциях на ее же оси имеет вид, аналогичный приведенному выше (12):

В дальнейшем последние выражения также, как и выражения (12), будем использовать в следующем виде:

где под следует, очевидно, понимать составляющие:

Очевидно, что с учетом (12) приведенные выше выражения (4) могут быть представлены следующим образом:

В приведенных выше выражениях - это составляющие абсолютной угловой скорости объекта в проекциях на оси ЛСК Ох_лy_лz_л.

Представляется целесообразным кратко описать физическую суть приведенных выше дифференциальных уравнений и, прежде всего, уравнений, описывающих характер изменения углов визирования цели (20).

По определению известно, что характер изменения углов визирования цели определяется угловой скоростью вращения ЛСК относительно ССК. Первые два члена в рассматриваемых уравнениях, а именно, - и , являются соответствующими компонентами угловой скорости вращения ЛСК относительно ИСК OXYZ. И только после вычитания из них составляющих угловой скорости и , правые части рассматриваемых дифференциальных уравнений приобретают ту физическую суть, которую они должны иметь по определению относительных угловых скоростей .

Входящие в (20) составляющие абсолютной линейной скорости движения цели, в соответствии с теоремой Кориолиса [3], в общем случае, описываются векторным дифференциальным уравнением вида:

в котором - вектор абсолютной угловой скорости вращения подвижной, в рассматриваемом случае, лучевой системы координат.

В проекциях на ее оси приведенное выше векторное уравнение может быть представлено следующими дифференциальными уравнениями:

Подстановка в них соответствующих составляющих абсолютной угловой скорости (12) или (18) приведет их к следующему, удобному для дальнейшего рассмотрения виду:

Дифференциальные уравнения, описывающие характер изменения локальных производных от составляющих скорости, представленных ускорениями , для рассматриваемого краткосрочного режима наблюдения, не превышающего 13-15 сек, из которых 3 сек - это собственно режим полноценной - с измерением дальности, привязки, а 10-12 сек - модифицированный режим программного сопровождения цели, реализуемого на фоне непрерывающегося ее углового сопровождения (в режиме ручного PC или автоматического АС сопровождения), могут представлены, либо в виде:

либо в виде дифференциальных уравнений, характерных для цветного шума первого порядка с ненулевым математическим описанием:

где i=х_Л, y_Л, z_Л, μ_i, σ_i - традиционные для случайных шумов рассматриваемого типа параметры, характеризующие изменчивость (μ_i) и интенсивность (σ_i) процесса; W_i - белый шум единичной интенсивности.

Объединяя приведенные выше уравнения (20), (23) и (24), получим следующую замкнутую систему дифференциальных уравнений 9-го порядка, в общем случае, нелинейную, представленную в нормальной форме Коши:

Выбор ЛСК в качестве подвижной не случаен, поскольку только в этом случае достаточно просто может быть редуцирована полученная выше модель относительного движения цели (26) путем разделения ее на дальномерный канал с вектором состояния и канал углового сопровождения цели с вектором состояния , что, по окончании режима привязки к цели, не прерывая ее углового сопровождения, позволит реализовать эффективную процедуру субоптимального оценивания по измерениям текущих углов ϕ_y, ϕ_z визирования цели.

Приведенная выше модель относительного движения объекта и цели в проекциях на оси лучевой системы координат предназначена для синтеза структуры оптимального фильтра-идентификатора параметров относительного движения цели.

При этом в качестве сигналов измерения на 3-х секундном интервале привязки к цели должны использоваться измеренные ОПС (ОЛС) наклонная дальность до цели и текущие значения углов ϕ_y, ϕ_z ее визирования, которые, как правило, наблюдаются на фоне случайных шумов измерения :

z₃=ϕ_z+V_y,

Если все представленное выше дополнить приведенной в общем виде матрицей оптимальных коэффициентов усиления:

и расписать матричное дифференциальное уравнение вида:

то с учетом разработанной модели сообщения (26) и сигналов измерения (27), получим систему дифференциальных уравнений 9-го порядка, структурируя которую можно получить структурную схему оптимального фильтра-идентификатора параметров движения цели, реализуемого на основе оптимальной дискретной процедуры оптимальной фильтрации и идентификации постоянно обновляющихся последовательностей сигналов (27), измеряемых ОПС в режиме ручного или автоматического сопровождения цели.

Система дифференциальных уравнений (26) в случае ее дискретного представления будет иметь следующий вид:

В приведенной системе дискретных уравнений под Δϕ_yk и Δϕ_zk следует понимать:

Аналогичная процедура должна использоваться и при численном интегрировании составляющих и , в которых присутствуют члены, определяемые угловыми скоростями изменения углов ориентации объекта.

По окончании режима привязки к цели, не прерывая ее аппаратного углового сопровождения, вместо прогноза параметров движения цели, реализуют субоптимальную процедуру оптимального оценивания, для чего, полученные по ее результатам значения оценок и используют для их прогноза в соответствии с приведенными выше дискретными уравнениями, в которых упомянутые оценки используются, как начальные условия.

При этом в качестве оценок и на первом такте прогноза используют их значения, полученные в процессе привязки к цели, а затем - текущие значения оценок, полученные в процессе оптимальной фильтрации и идентификации сигналов ϕ_y и ϕ_z углового сопровождения цели.

Для эффективной реализации последней используют прогнозируемые значения оценок , а сама процедура идентификации текущих углов визирования цели должна осуществляться - в соответствии с редуцированной моделью ее углового сопровождения, имеющей вид:

При этом в качестве сигналов измерения используют текущие значения измеренных углов визирования цели, которые, также, как и ранее (27), наблюдаются на фоне случайных шумов измерения V_y, V_z (см. (35), (36)):

Синтез структуры оптимального фильтра-идентификатора для режима углового сопровождения цели с прогнозом текущего значения наклонной дальности и скорости сближения с целью может быть осуществлен в соответствии с приведенной выше его, моделью сообщения (30) и сигналами измерения (31).

Матрица оптимальных коэффициентов усиления для рассматриваемого режима оптимальной фильтрации и идентификации имеет вид:

Система дифференциальных уравнений (30) в случае ее дискретного представления, по аналогии с системой (29), будет иметь следующий вид:

Разработанная процедура привязки к подвижной наземной цели, реализуемая в обеспечение высокоточного применения неуправляемого АСП, включает в себя этап активного, с измерением наклонной дальности до цели, и аппаратного, с измерением текущих углов ее визирования ϕ_y, ϕ_z, сопровождения с параллельно реализуемой оптимальной процедурой фильтрации и идентификации измеряемых на 3-х секундном интервале привязки сигналов , ϕ_y, ϕ_z с оцениванием оптимальных относительных координат местоположения цели и параметров ее движения в проекциях на сои лучевой системы координат ЛСК , по окончании которого, что определяется завершением работы лазерного дальномера прицельной системы, оптимальный фильтр-идентификатор модифицируют и переводят в режим пассивного, без измерения дальности, углового сопровождения цели, при этом его размерность с 9-го порядка уменьшается до 6-го за счет исключения 3-х параметров канала наклонной дальности, а именно, , . Редуцированный таким образом фильтр работает по постоянно обновляющейся последовательности измеренных углов ϕ_y, ϕ_z визирования цели, а в результате рекуррентной процедуры их и