Способ определения качества резиновой изоляции кабелей

Способ определения качества резиновой изоляции кабелей

Иллюстрации

Показать все

Реферат

Изобретение относится к области силовых кабелей, в частности резиновой изоляции кабелей, и может быть использовано для диагностики и оценки качества резиновой изоляции кабелей.

В мировой практике до сих пор не создана система профилактических испытаний кабельной изоляции силовых кабелей неразрушающими методами, которая позволила бы оценивать остаточный ресурс и прогнозировать вероятность выхода кабеля из строя в процессе его эксплуатации. Осуществляется только эпизодический контроль сопротивления штатными приборами. Практикуемые на энергетических предприятиях испытания высоким напряжением, в ходе которых происходит пробой изоляции в «слабых» участках (с последующей заменой пробитых отрезков), например на судах, категорически запрещен и не может быть применим.

Тем более, что подобные процедуры не могут предотвратить аварийные ситуации и не дают информации об остаточном ресурсе кабеля и, кроме того, могут сами по себе приводить к ухудшению состояния изоляции, поскольку испытательное напряжение значительно превышает рабочее (эксплуатационное) напряжение.

В связи с этим актуальным является необходимость разработки способа неразрушающего контроля и остаточного ресурса изоляции кабелей, который основывается на анализе физических свойств изоляции кабеля.

Попытки разработки подобного способа были сделаны в работах С.Н. Койкова, Сажина Б.И. (Койков C.H., Цикин А.Н. Электрическое старение твердых диэлектриков. - Л.: Энергия, 1968 - 184 с.; Сажин Б.И. Электрические свойства полимеров. - Л.: Химия. 1986 г.) и других. Результаты исследований позволили выдвинуть гипотезы о старении керамических конденсаторов, кабелей с полиэтиленовой, бумажно-пропитанной изоляцией и т.п.

Контроль надежности и оценка остаточного ресурса силовых кабелей может быть осуществлены на основе измерения абсорбционных характеристик, динамических вольтамперных характеристик, реверсивных и термостимулированных токов и другими технически сложно реализуемыми методами (Казарновский Д.М., Тареев Б.М. Испытания электроизоляционных материалов, не имеющие перспективы применения в реальных условиях эксплуатации кабелей (Пошерстник М.Ю., Салютина М.А. Справочник по судовым кабелям и проводам. - Л.: Судостроение, 1966. - 251 с.).

Наиболее перспективным является выявление диагностических параметров изоляции - физических свойств, которые изменяются в процессе старения изоляции.

Известен способ определения качества резиновой изоляции кабелей (а.с. СССР №1394174, опубл. 07.05.1988), заключающийся в том, что прикладывают постоянное испытательное напряжение между жилой кабеля и измерительным электродом, измеряют зависимость тока через изоляционное покрытие от температуры, а о качестве изоляции судят по особенностям зависимости тока от температуры. После длительной эксплуатации на зависимости тока от температуры проявляется точка излома, которая смещается в область более низких температур. Способ позволяет своевременно устранять состарившиеся локальные участки кабельной сети.

К недостаткам известного способа относится необходимость прикладывания электродов и электрического напряжения, создание условий для монотонного увеличения температуры образца кабелей в процессе испытаний, что нельзя осуществить непосредственно в процессе эксплуатации, тем более под напряжением кабеля.

Задача изобретения заключается в разработке простого способа определения качества изоляции кабелей непосредственно в реальных условиях их эксплуатации, в т.ч. под напряжением.

Технический результат, на достижение которого направлено заявляемое изобретение, состоит в создании простого способа определения качества резиновой изоляции кабелей непосредственно в процессе их эксплуатации, в т.ч. под напряжением.

Для достижения указанного технического результата в заявляемом способе используют диагностический параметр - твердость изоляции Н, которую измеряют стандартными приборами для измерения твердости по методу Шора. Твердость H измеряют переносным измерителем твердости, например ТН-200, значения которого (в пределах от 0 до 100) приводятся в единицах HSA.

Сущность изобретения заключается в следующем.

Согласно техническим условиям одним из критериев работоспособности кабелей после истечения срока службы является отсутствие на поверхности шланговой оболочки трещин по длине.

В процессе эксплуатации за счет протекающих химических реакций кабель теряет эластичность, гибкость и становится жестким. На его оболочке и изоляции жилы возникает первоначально сетка мелких трещинок, а затем, окончательно, трещины, открывающие доступ влажному воздуху, загрязнениям вплоть до металлической жилы (при этом следует заметить, что в отсутствие загрязнений и в сухом воздухе электрическое сопротивление кабеля с трещинами в объеме изоляции может оставаться относительно повышенным, но оно резко падает во влажной или агрессивной среде).

Анализ и опыт эксплуатации кабелей с резиной изоляцией показывает, что срок службы кабелей ограничивается фактически временем появления трещин на поверхности шланговой изоляции кабеля.

Таким образом, критерием старения является образование трещин на поверхности шланговой изоляции и изоляции жилы.

Для экспресс-анализа технического состояния кабелей необходимо разработать методику оценки диагностического параметра, который изменяется со временем по мере старения изоляции и непосредственно связан с процессом трещинообразования.

Подобным диагностическим параметром, по мнению авторов, является твердость изоляции, которая, как показывает практика, существенно изменяется в процессе старения изоляции.

Следует учитывать, что одноразовое измерение твердости шланговой изоляции кабеля или изоляции жилы недостаточно для оценки технического состояния кабелей по следующей причине.

Шланговую изоляцию и изоляцию жилы кабелей выполняют из полимерного материала - эластомера, состав которого регламентирован техническими условиями. Несмотря на идентичность механических и электрических характеристик в целом, локальные участки кабелей отличаются друг от друга по своим показателям и характеризуются статистическими характеристиками, обусловленными естественным разбросом данных.

При анализе заявленного диагностического параметра следует учитывать, что старение изоляции кабелей происходит неодинаково в разных точках поверхности по всей длине кабеля. Это связано с вероятностными процессами протекающих химических реакций. Т.е. естественным является разброс значений твердости в различных точках как исходного, так и состаренного кабелей.

В связи с этим при исследовании параметров твердости выделенного участка кабелей осуществляют многократные измерения (n измерений) и фиксируют локальные значения твердости, обозначаемые как твердость шланговой изоляции H_{i из.ш} и твердость H_{i из.ж} изоляции жилы. С учетом статистического разброса данных полученную совокупность значений твердости (выборку) обрабатывают известными статистическими методами для оценки статистических параметров: среднего значения твердости (H_{i из.ш} и H_{i из.ж}), квадратического отклонения, абсолютной погрешности ΔН и др., а также статистических функций: функции распределения твердости F(H), функции плотности распределения твердости .

Предлагаемый способ определения качества резиновой изоляции кабелей иллюстрируется чертежами, представленными на фиг. 1-4.

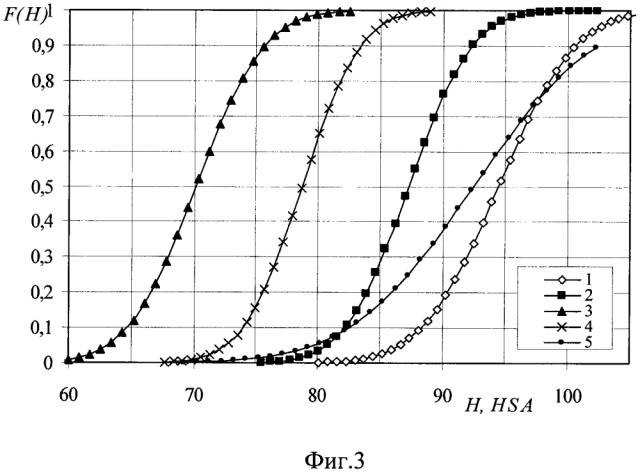
На фиг. 1 представлены данные расчета стандартных функций F(H), для твердости шланговой изоляции кабеля КНР 3×4 мм², на фиг. 2 - данные расчета стандартных функций F(H), для твердости изоляции жилы кабеля КНР 3×4 мм², на фиг. 3 - график зависимости функции распределения F(H) от твердости изоляции кабелей, на фиг. 4 - график зависимости функции плотности распределения от твердости изоляции кабелей.

Способ осуществляют следующим образом.

Выбирают участок кабельной трассы для анализа шланговой изоляции H_{i из.ш} и изоляции жилы H_{i из.ж} кабеля. Производят на выбранном участке кабельной трассы замеры твердости в количестве 25-30, которое определяется с учетом проведения статистического анализа. Причем измерение твердости изоляции жилы кабеля проводят на участке с оголенным шлангом, например вблизи контактных соединений, светильников и др., т.е. в тех местах, где есть доступ и к самой изоляции жилы кабеля. Затем проводят математическую обработку полученных данных.

Математическая обработка данных может быть осуществлена стандартным методом путем расчета среднего значения H, абсолютной погрешности ΔH, при учете коэффициента t_n Стьюдента (вероятность Р=0,95), а также расчетом функции распределения твердости F(H) и функции распределения плотности твердости анализируемой выборки.

Пример

Определение качества состаренной шланговой изоляции кабеля КНР 3×4 мм².

В процессе испытаний неоднократно измеряют значения твердости шланговой изоляции H_{i из.ш} кабеля и изоляции жилы H_{i из.ж} кабеля анализуемой выборки, представленной соответственно в таблицах (фиг. 1, 2), так что каждое значение твердости H_i - случайная величина, принимающая одно из возможных значений твердости в пределах определенного промежутка от H_мин до H_мах в результате испытаний.

Совокупность значений выборки (фиг. 1, 2), как значений случайной величины, образует статистический ряд, в нашем случае 2 ряда. Для анализа такого ряда можно использовать разнообразные числовые характеристики статистики (имеют функции в пакете Excel): среднее значение H (математическое ожидание), стандартное (квадратическое) отклонение σ и т.д. Характеристикой случайной величины H является закон распределения, имеющий две формы представления:

- функция распределения F(H) твердости, определяющая вероятность появления случайной величины, принимает значения от 0 до 1 (интегральная функция);

- функция плотности распределения твердости - - первая производная от функции распределения (дифференциальная функция), показывающая вероятность попадания случайной величины в заданный интервал и какие значения случайной величины наиболее вероятны.

Определение форм нормального распределения средствами Excel реализуют с помощью стандартных статистических функций. Например, функция НОРМРАСП (х; H; σ; интегральная), где х - значение случайной величины H_i, для которой определяют F(x) и. Параметр "интегральная" определяет форму распределения, для которой определяется значение (F(x) - "ИСТИНА"; - "ЛОЖЬ").

Определение функции распределения твердости и плотности распределения твердости может быть пояснено на примере данных, представленных в таблицах (фиг. 1, 2):

1) производят испытания параметров твердости выборки H_{i из.ш} и H_{i из.ж};

2) рассчитывают средние значения H (функция "СРЗНАЧ") и стандартное отклонение σ ("СТАНДОТКЛОН");

3) находят пределы изменения случайной величины с учетом закона трех сигм (генеральная совокупность): H_мин=H-3σ; H_мах=H+3σ, округляют полученные значения;

4) вычисляют шаг δH изменения случайной величины для определения интервала изменения генеральной совокупности: δH=(H_мах-H_мин)/n, где n - количество значений в возможном интервале, задаваемое при испытании;

5) записывают вероятные значения изменения величины H_{i из.ш} и H_{i из.ж} через шаг δH от H_мин до H_мах;

6) вычисляют значения функции распределения F(H) твердости и плотности распределения твердости с помощью функции НОРМРАСП, причем функции F(H) и являются стандартными функциями программы Excel, с помощью которой их вычисляют;

7) строят графики зависимости функции F(H) и плотности распределения от твердости с помощью мастера диаграмм.

Результаты расчета стандартных функций для твердости шланговой изоляции КНР 3×4 мм² представлены в таблице (фиг. 1), результаты расчета стандартных функций для твердости изоляции жилы кабеля КНР 3×4 мм² представлены в таблице (фиг. 2). На основании рассчитанных данных (фиг. 1 и фиг. 2) построены графики зависимостей функции F(H) и плотности распределения от твердости для шланговой изоляции кабеля КНР 3×4 мм² (кривая 2 на фиг. 3, 4) и изоляции жилы кабеля КНР 3×4 мм² (кривая 3 на фиг. 3, 4).

Таким образом, анализ данных (фиг. 3, 4, кривая 2) показывает, что трещины в шланговой изоляции исследуемого кабеля КНР появляются в том случае, когда более 50% результатов выборки имеют значения более H_из.ш>95-97 HSA.

Аналогично, показано, что трещины в изоляции жилы исследуемого кабеля КНР появляются в том случае, когда более 50% результатов выборки имеют значения более H_из.ж>89-90 HSA (фиг. 3, 4, кривая 3).

Аналогичным образом была исследована резиновая изоляция других кабелей, результаты представлены кривыми 1, 4, 5 на фиг. 3, 4.

На фиг. 3, 4 обозначены позициями графики для:

1 - изоляции жилы (более 40 лет старения с трещинами); 2 - шланговой изоляции кабеля (без трещин); 3 - изоляции жилы внутри шланга (без трещин); 4 - изоляции жилы вне шланга на воздухе (без трещин); 5 изоляции жилы вне шланга на воздухе (с трещинами).

Например, для полностью разрушенной резиновой изоляции жилы (кривая 1) более 50% значений лежат в пределах Н_из.ж>95 HSA.

Шланговая изоляция кабеля КНР (кривая 2) после 25 лет хранения при комнатных условиях практически утратила упругость (95% значений лежат в пределах Н_из.ш.<92 HSA), но видимых поперечных трещин не наблюдается.

Изоляция жилы кабеля КНР, находящаяся в ненарушенной шланговой изоляции (кривая 3), имеет относительно хорошую упругость при среднем значении твердости Н_из.ж.ш=70 HSA (для исходной изоляции жилы Н_из.ж=66,3 НА), а максимальные значения твердости не превышают Н_{из.ж.мах}=82 HSA. (фиг. 3, 4).

Изоляция жилы, находящаяся на воздухе вне шланга (фиг. 3, 4 кривые 4 и 5), потеряла упругость, причем 33% изоляции жилы (одна жила из трех) имеет выраженные поперечные трещины; при этом более 50% значений имеют твердость более Н_из.ж.=92,5 HSA (кривая 5). Изоляция жилы, не имеющая трещин, имеет 50% значений выше среднего значения (Н=78, 7 HSA), при этом большинство значений твердости лежит в пределах H<92 HSA.

Таким образом, трещины в шланговой изоляции исследуемого кабеля появляются в том случае, когда более 50% результатов выборки имеют значения более H_из.ш>95-97 HSA.

Аналогично показано, что трещины в изоляции жилы исследуемого кабеля КНР появляются в том случае, когда более 50% результатов выборки имеют значения более Н_из.ш>89-90 HSA.

Использование предлагаемого способа определения качества резиновой изоляции кабеля позволяет провести экспресс анализ участков кабельных трасс, что приводит к увеличению эксплуатационной надежности, электро- и пожаробезопасности электрических сетей. Достоинством данного способа является возможность определения качества шланговой изоляции и изоляции жилы кабеля непосредственно в процессе эксплуатации, в том числе под напряжением.

1. Способ определения качества резиновой изоляции кабелей, характеризующийся тем, что выбирают участок кабельной трассы для анализа твердости шланговой изоляции и изоляции жилы, производят на выбранном участке n количество замеров твердости шланговой изоляции и изоляции жилы, проводят математическую обработку полученных данных, для этого рассчитывают средние значения твердости Н и стандартное отклонение σ, находят пределы изменения случайной величины Н с учетом закона трех сигм (генеральная совокупность) по формулам:

Н_мин=Н-3σ; Н_мах=Н+3σ,

округляют полученные значения, вычисляют шаг δН изменения случайной величины Н для определения интервала изменения генеральной совокупности по формуле:

δН=(Н_мах-Н_мин)/n,

где n - количество замеров, задаваемое при испытании, записывают вероятные значения изменения величины H_i через шаг δН от Н_мин до Н_мах, вычисляют значения функции распределения твердости F(H) и плотности распределения твердости и строят графики зависимости этих функций от твердости, по которым определяют качество резиновой изоляции кабелей.

2. Способ по п. 1, характеризующийся тем, что функция распределения твердости F(H) определяет вероятность появления случайной величины Н и принимает значения от 0 до 1 (интегральная функция).

3. Способ по п. 1, характеризующийся тем, что функция плотности распределения твердости - первая производная от функции распределения (дифференциальная функция) показывает вероятность попадания случайной величины Н в заданный интервал и какие значения случайной величины Н наиболее вероятны.