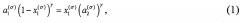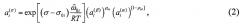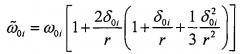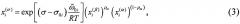Способ определения состава поверхностного слоя наночастицы, находящейся в матрице в бинарной системе

Способ определения состава поверхностного слоя наночастицы, находящейся в матрице в бинарной системе

Иллюстрации

Показать все

Реферат

Изобретение относится к физико-химическим анализам, более конкретно, к установлению зависимости состава поверхностного слоя двухкомпонентной наночастицы сферической формы, находящейся в двухкомпонентной матрице в равновесных условиях, в зависимости от радиуса наночастицы и состава матрицы и наночастицы.

Известны способы определения состава поверхностного слоя с использованием зондирования поверхности электронами, ионами, атомами, рентгеновским и ультрафиолетовым излучением и другими [1]. Они пригодны для количественного анализа свободных поверхностей, доступных прямому зондированию, или установления распределения компонентов по глубине образца путем послойного анализа, но они не могут быть использованы для определения состава скрытой границы наночастица - матрица.

Известен способ спектроскопии обратного рассеяния первичных ионов (обычно Не⁺ с энергиями 100 кэВ-5 МэВ и глубинами 0,1-30 мкм) [1]. Однако этот способ вообще не пригоден для количественного анализа тонкой (единицы или десятки нанометра) границы раздела наночастицы и матрицы.

Наиболее близким к предлагаемому является способ определения состава поверхностного слоя на границе раздела твердого и жидкого растворов в двухкомпонентной системе [2].

Этот способ легко реализуется на практике и позволяет получать данные о составе межфазного слоя на границе взаимно насыщенных растворов при разных температурах.

Однако известный способ применим только для границы раздела твердых и жидких растворов макроскопических размеров. В случае, когда одна из фаз находится в нанометровом диапазоне, способ практически нереализуем. Кроме того, этот способ вообще не пригоден для измерения состава поверхностного слоя на границе раздела двух взаимнонасыщенных твердых растворов.

Задачей изобретения является расширение области применения способа путем обеспечения возможности определения состава поверхностного слоя на границе двухкомпонентной наночастицы и двухкомпонентной матрицы, находящихся в равновесном состоянии, в зависимости от радиуса сферической наночастицы.

Поставленная цель достигается тем, что одним из известных методов экспериментально определяют состав наночастицы и матрицы, а также средний радиус наночастицы сферической формы и по формуле:

где , - концентрация (мольная доля) первого компонента в поверхностном слое,

где и - термодинамическая активность i-го компонента (i=1, 2) в наночастице и матрице соответственно, σ - поверхностное натяжение на границе наночастицы и матрицы в бинарной системе, σ_0i - поверхностное натяжение на границе фаз α и β в однокомпонентной системе (чистого i-го компонента), , ω_0i, δ_0i - молярная поверхность и параметр Толмена на границе фаз α и β чистого i-го компонента, , - молярный объем для чистого i-го компонента в фазе ν (ν=α,β,σ), Т - температура (в Кельвинах), R - универсальная газовая постоянная, находят концентрацию первого компонента в поверхностном слое . Концентрация второго компонента в поверхностном слое определяется из соотношения . Формула (1) получена в рамках подхода регулярных растворов, который обычно используется при рассмотрении свойств наночастиц, находящихся в матрице [3].

Задача упрощается для случая, когда фазы α, β и σ можно считать идеальными растворами (, , ). В этом случае расчет ведется по формуле:

Предлагаемый способ осуществляется следующим образом.

Одним из известных методов определяют концентрацию одного из компонентов в наночастице и матрице , а также средний радиус наночастицы r. Такими методами, в частности, могут являться метод томографического атомного зондирования, метод трансмиссионной электронной микроскопии [3] и некоторые другие.

Значения и , необходимые для расчета по формуле (2), находятся с учетом термодинамических характеристик растворов, в частности, в локально-координационном приближении [3], в зависимости от состава , , температуры и радиуса кривизны наночастицы сферической формы r. При этом размерная зависимость параметра квазихимического взаимодействия в фазах α и β учитывается по известной зависимости координационного числа от размера [4]. Поверхностное натяжение на границе наночастицы и матрицы в бинарной системе σ, входящее в (2), рассчитывается в соответствии с [5]. Значения σ_0i в зависимости от r и δ_0i, находятся, следуя [6] и [7] соответственно.

Пример 1. В качестве образца выбирается сплав, склонный к распаду с выделением дисперсных частиц, например, сплавы Fe и Сr, для которых и рассмотрим конкретное выполнение предлагаемого способа. После стандартных процедур (гомогенизация, закалка, высокотемпературный отпуск), выполняемых по известной технологии, имеет место распад пересыщенного твердого раствора с выделением дисперсных частиц [8]. По одной из известных методик (например, томографического атомного зондирования [9]) изучаются изменения микроструктуры сплава, при выбранной температуре. Определяются зависимость концентрации хрома , среднего радиуса выделения (преципитата) r, а также состава матрицы от времени отжига. При достижении термодинамически равновесного состояния эти величины перестают зависеть от времени. Полученные таким образом значения [9] для сплава Fe-Cr приведены в таблице.

Значения и , входящие в (2), вычисляются с использованием , , а также средних энергий парного взаимодействия ε_Fe-Fe=-1,072 эВ, ε_Cr-Cr=-1,025 эВ, ε_Fe-Cr=-0,998 эВ, приведенные в [3].

Технический результат заключается в том, что предлагаемый способ определения поверхностного натяжения наночастиц, находящихся в матрице, пригоден для всех температурных и концентрационных областей фазового равновесия двухкомпонентных твердых растворов, а также любых размеров наночастиц; применим для различных типов неассоциированных твердых тел (металлических, полупроводниковых, диэлектрических); позволяет выявить влияние наноразмерных эффектов на состав поверхностного слоя между двумя растворами, находящимися в конденсированном состоянии в равновесных условиях; является неразрушающим способом.

Литература

1. Вудраф Д., Делчар Т. Современные методы исследования поверхности. Москва, Мир, 1989, 568 с.

2. Авторское свидетельство SU 1173261, кл. G01N 13/00.

3. Львов П.Е., Светухин В.В., Обухов Термодинамика фазового равновесия бинарных сплавов, содержащих наноразмерные преципитаты. Физика твердого тела, 2011, том 53, вып. 2, с. 394-399.

4. Frenkel A.I., Yevick A., Cooper Ch. And Vasic R. Annu Rev. Anal. Chem (2011) 4; 23-29.

5. Шебзухова M.A., Шебзухов A.A. Патент РФ №2585514 от 06.05.2016 г. Способ определения поверхностного натяжения двухкомпонентной наночастицы, находящейся в матрице.

6. Шебзухов З.А., Шебзухова М.А., Шебзухов А.А. Поверхность, синхротронные и нейтронные исследования, 2009, №11, с. 102.

7. Шебзухова М.А., Шебзухов А.А. ФТТ, 54, 1, 173 (2012).

8. Григорович В.К. Жаропрочность и диаграммы состояния. М., Металлургия, 1969, 324 с.

9. Novy S., Pareige P., Pareige С.J. Nucl. Mater, т. 384, 96, 2009.

Способ определения состава поверхностного слоя двухкомпонентной наночастицы сферической формы в матрице, отличающийся тем, что, с целью установления размерной зависимости состава поверхностного слоя наночастицы, сплав, содержащий наноразмерные частицы, представленный листовым материалом, содержащим дисперсную частицу в дисперсионной среде, подвергают термическому отжигу, определяют состав наночастицы и матрицы, а также средний радиус наночастицы и по формуле

где , - концентрация (мольная доля) первого компонента в поверхностном слое, и - термодинамические активности компонентов в поверхностном слое, определяемые через аналогичные величины наночастицы и матрицы, а также поверхностное натяжение, находят искомую величину.