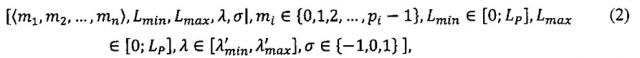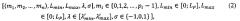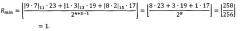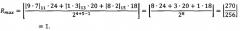Способ организации выполнения операции умножения двух чисел в модулярно-логарифмическом формате представления с плавающей точкой на гибридных многоядерных процессорах

Способ организации выполнения операции умножения двух чисел в модулярно-логарифмическом формате представления с плавающей точкой на гибридных многоядерных процессорах

Иллюстрации

Показать все

Реферат

Изобретение относится к вычислительной технике и предназначено для выполнения операции умножения чисел, представленных в модулярно-логарифмическом формате с плавающей точкой на гибридных многоядерных процессорах.

Известен способ организации выполнения операции умножения двух чисел в модулярно-позиционном формате представления с плавающей точкой на универсальных многоядерных процессорах (A.C. RU №2509345, БИ №7, 10.03.2014), в котором операция умножения t-разрядных позиционных мантисс сомножителей заменяется n параллельно выполняемыми операциями умножения q-разрядных знакопозиций чисел в системе счисления в остаточных классах. Недостаток данного способа состоит в том, что не определено, каким образом выявляются ситуации переполнения диапазона представления модулярных мантисс при выполнении операции умножения и выполняется процедура масштабирования мантисс, таким образом, способ (A.C. RU №2509345, БИ №7, 10.03.2014) может быть использован для выполнения операции умножения не для всех операндов из заявленного диапазона представления.

Наиболее близким к заявленному способу является способ организации выполнения операции умножения двух чисел в модулярно-позиционном формате (Исупов К.С., Мальцев А.Н. Способ представления чисел с плавающей точкой большой разрядности, ориентированный на параллельную обработку //Вычислительные методы и программирование: новые вычислительные технологии. 2014. Т. 15, №4. С. 631-643), в котором масштабирование мантиссы осуществляется методом, использующим таблицы поправочных коэффициентов с применением интервально-позиционных характеристик. Недостаток данного способа состоит в том, что необходимо хранить таблицы поправочных коэффициентов большого размера, а также использовать вычислительные устройства с плавающей точкой для вычисления интервальной позиционной характеристики.

Техническим результатом применения способа организации выполнения операции умножения двух чисел в модулярно-логарифмическом формате представления с плавающей точкой на гибридных многоядерных процессорах является оптимизация выполнения операции умножения в раз, где q - разрядность знакопозиций чисел в системе счисления в остаточных классах, за счет использования только целочисленных операций при умножении, проверке выхода за границы диапазона, масштабировании модулярных мантисс степенью двойки, при этом не требуется использования операций с плавающей точкой и подстановочных таблиц. Минимальное время выполнения операции умножения предложенным способом равно минимальному времени выполнения операции умножения способом (A.C. RU №2509345, БИ №7, 10.03.2014), при этом способ может быть применен для умножения любых операндов из заявленного диапазона представления, в чем заключается универсальность предлагаемого способа.

Описание способа организации выполнения операции умножения двух чисел в модулярно-логарифмическом формате представления с плавающей точкой на гибридных многоядерных процессорах: реализация способа осуществляется посредством подачи набора электрических, нейронных либо других сигналов на устройства управления каждого вычислительного ядра многоядерного гибридного процессора, которые, в соответствии с данными сигналами, формируют управляющие команды для операционных устройств соответствующих вычислительных ядер.

В позиционных двоичных форматах с плавающей точкой стандарта IEEE-754 любое вещественное число представляется трехэлементным набором:

где М - рациональная мантисса, е - порядок числа, e_min=2-2^ν-1 и e_max=2^ν-1-1, S-знак числа.

Величина чисел, записанных в таком формате, выражается формулой -1^S⋅М⋅2^е. Машинными представлениями чисел вида (1) являются (ν+t+1)-разрядные двоичные векторы (Sr_ν-1…r₂r₁d_t…d₂d₁), где разряды с d₁ по d_t отводятся под представление рациональных двоичных мантисс М=d_td_t-1…d₂d₁, разряды с r₁ по r_ν отводятся под представление целочисленных двоичных порядков е, записанных в форме с избытком Е=r_νr_ν-1…r₂r₁=е+e_max, разряд S выражает знак числа.

Определим целочисленную мантиссу М'=d_td_t-1…d₂d₁ как t-разрядное неотрицательное целое двоичное число, такое, что М=М'⋅2^1-t. Определим перемещенный порядок λ как целое двоичное число со знаком, такое, что λ=е-t+1, где е - ν-разрядный порядок числа, представленного в двоичном формате (1).

Зададим n целочисленных положительных q-разрядных оснований системы остаточных классов p₁,р₂, …, p_n, таких, что ∀i₁, i₂∈{1, 2, …, n), i₁≠i₂: , q≤k, где - наибольший общий делитель для и , k - размер разрядной сетки процессора.

Целочисленную мантиссу М'=d_td_t-1…d₂d₁ преобразуем в систему остаточных классов с заданными основаниями р₁, p₂, …, p_n, получая тем самым модулярную мантиссу :

,

где m_i∈[0, р_i-1], i=1, 2, …, n - q-разрядные цифры (модулярные разряды) модулярной мантиссы , q - разрядность оснований p₁, p₂, …, p_n, - операция получения остатка от деления М' на i-ое основание p_i.

Определим ранг модулярной мантиссы как значение R, такое, что выполняется условие:

,

где - мультипликативная инверсия Р_i по модулю рi∈[1, n], n - количество модулей.

R∈[0,n-1] и вычисляется по формуле:

,

где - наибольшее целое, не превышающее

При условии, что 2^q-1<p_i<2^q, где q - разрядность оснований р₁, р₂, …, р_n, величина может быть вычислена по формуле , где w_i - s-разрядные весовые коэффициенты. Тогда величина ранга может быть вычислена по формуле:

.

Определим верхнюю и нижнюю границы величины ранга модулярного числа как

, ,

где , , при условии, что 2^q-1<р_i<2^q, - наибольшее целое, не превышающее , s - разрядность коэффициентов w_i.

Согласно теоретико-числовой теореме Эйлера мультипликативную инверсию , соответствующую сравнению , можно вычислить следующим образом

,

где ϕ(p_i) - функция Эйлера, равная количеству целых чисел в диапазоне [1, р_i], взаимно простых с р_i.

Пример. Вычислим значения мультипликативных инверсий P_i по модулям р_i для системы с основаниями: р₁=11, р₂=13, р₃=15:

; ϕ(11)=10; ;

; ϕ(13)=12; ;

; ϕ(15)=12;

Определим логарифмическую характеристику числа как значение двоичного логарифма от этого числа. Тогда логарифмическая характеристика модуля числа, представленного в формате [М, е, S], вычисляется следующим образом:

log₂(М'⋅2^1-t⋅2^е)=log₂(М')+е-t+1=log₂(М')+λ.

Определим интервальную логарифмическую характеристику мантиссы числа как целочисленный интервал [L_min, L_mах], нижняя и верхняя границы L_min, L_mах которого представлены r-разрядными двоичными числами без знака и вычисляются следующим образом:

L_min=[log₂(М')⋅2^r-h-1],

L_mах=L_min+1

где , - наибольшее целое, не превышающее , [log₂(М')⋅2^r-h-1] - наибольшее целое, не превышающее log₂(М')⋅2^r-h-1.

Диапазон представления нижней и верхней границ L_min, L_mах интервальной логарифмической характеристики:

; ,

где - значение нижней границы интервальной логарифмической характеристики диапазона представления модулярных мантисс , - наибольшее целое, не превышающее .

Таким образом, число с плавающей точкой вида (1) можно преобразовать к следующему модулярно-логарифмическому формату:

где 〈m₁, m₂, …, m_n〉 - набор знакопозиций (модулярных разрядов) модулярной мантиссы , λ- позиционный перемещенный порядок, представляющий собой целое двоичное число со знаком, L_min, L_max - границы интервальной логарифмической характеристики мантиссы числа, представляющие собой целые двоичные числа без знака, σ - знак числа, причем если σ=-1, то число отрицательное, σ=1 - положительное, σ=0 - машинный ноль.

Диапазон допустимых значений модулярных мантисс в системе остаточных классов с основаниями p₁, p₂, … , р_n определяется интервалом ; таким образом, t-разрядная позиционная мантисса М=d_td_t-1…d₂d₁ может быть представлена в системе остаточных классов набором из n взаимно независимых q-разрядных знакопозиций 〈m₁, m₂, …, m_n〉, причем q≈t/n (при условии, что все основания р₁, p₂, …, p_n q-разрядные).

Примеры преобразования позиционных чисел с плавающей точкой в модулярно-логарифмический формат: пусть числа представлены в 10-разрядном двоичном формате вида (1), в котором под смещенный порядок Е, отводится четыре бита (максимальный порядок е_max=2^4-1-1=7, соответственно е=Е-7), под дробную часть мантиссы - пять бит (т.е. t=6, причем целая часть d₆ рациональной мантиссы М в явном виде не записана) и под знак числа - один бит.Пусть для представления модулярных мантисс в модулярно-логарифмическом формате [〈m₁, m₂, …, m_n〉, λ, L_min, L_max, σ] используется три основания: р₁=11, р₂=13, р₃=15. Диапазон представления чисел Р=11⋅13⋅15=2145. Разрядность оснований q=4, разрядность интервальной логарифмической характеристики r=5.

Пример 1: необходимо перевести число X=3.3125₁₀=[1.65625, 1, 0]=-1⁰⋅1.65625⋅2¹, представленное в двоичном формате [М, е, S], в модулярно-логарифмический формат [〈m₁, m₂, …, m_n〉, L_min, L_max, λ, σ].

С учетом принятых характеристик двоичного формата [М, е, S], число X будет записано в памяти ЭВМ в виде двоичного вектора 〈0100010101〉. Для его преобразования в модулярно-логарифмический формат (2) необходимо выполнить следующие действия:

1. Выделить составные части числа X: знак числа S=0, дробная часть рациональной мантиссы d₅…d₂d₁=10101₂, смещенный (избыточный) порядок Е=1000₂=8.

2. Восстановить целую часть d₆ мантиссы М=d₆d₅…d₂d₁:d₆=1, т.к. Е>0, следовательно, М=1.10101₂.

3. Определить порядок е: е=Е-е_max=8-7=1, т.к. Е>0.

4. Определить знак σ, перемещенный позиционный порядок λ и целочисленную мантиссу М': σ=1, λ=е-t+1=1-6+1=-4, М'=d₆d₅…d₂d₁=110101₂=53.

5. Найти модулярную мантиссу : .

6. Вычислить интервально-логарифмическую характеристику мантиссы L_min, L_mах: L_min=[log₂(53)⋅2^5-3-1]=11, L_max=11+1=12.

В результате получается число X, представленное в модулярно-логарифмическом формате с плавающей точкой: X=[〈9, 1, 8〉, 11, 12, -4, 1].

Пример 2: необходимо перевести число X=0.02783203125₁₀=[1.78125, -5, 1]=-1¹⋅1.78125⋅2^-5 из двоичного формата [М, е, S] в модулярно-логарифмический формат [〈m₁, m₂, …, m_n〉, L_min, L_max, λ, σ].

С учетом принятых характеристик двоичного формата [М, е, S], число X будет записано в памяти ЭВМ в виде двоичного вектора 〈1000111001〉. Для его преобразования в модулярно-логарифмический формат (2) необходимо выполнить следующие действия:

1. Выделить составные части числа X: знак числа S=1, дробная часть d₅…d₂d₁=11000₂, смещенный порядок Е=0001₂=1.

2. Восстановить целую часть d₆ мантиссы М=d₆d₅…d₂d₁:d₆=1, т.к. Е>0, следовательно, М=1.11001₂.

3. Определить порядок е. е=е_min=1-7=-6, т.к. Е=0.

4. Определить знак σ, перемещенный порядок λ и целочисленную мантиссу М': σ=-1, λ=e-t+l=-6-6+1=-11, М'=d₆d₅…d₂d₁=111001₂=57.

5. Найти модулярную мантиссу :

6. Вычислить интервально-логарифмическую характеристику мантиссы L_min, L_max: L_min=log₂(57)⋅2^5-3-1]=11, L_max=11+1=12.

В результате получается число X, представленное в модулярно-логарифмическом формате с плавающей точкой: X=[〈2, 5, 12〉, 11, 12, -11, -1].

Алгоритм 1. Вычисление ранга числа, представленного в модулярно-логарифмическом формате.

Пусть - число, представленное в модулярно-логарифмическом формате с плавающей точкой, где - модулярная мантисса числа А. Для того чтобы найти ранг R модулярной мантиссы , необходимо:

1. Вычислить значение минимальной величины ранга R_min модулярной мантиссы : , где , , мультипликативная инверсия Р_i по модулю р_i, , - наибольшее целое, не превышающее , - наибольшее целое, не превышающее , s - разрядность , при условии, что 2^q-1<рi<2^q, s>1+log₂n.

2. Вычислить значение максимальной величины ранга R_max модулярной мантиссы : где , - мультипликативная инверсия Р_i по модулю р_i, , - наибольшее целое, не превышающее , - наибольшее целое, не превышающее , s - разрядность , при условии, что 2^q-1<рi<2^q, s>1+log₂n.

3. Если R_min=R_max, то R=R_min, иначе выполнить сравнение: если , то есть значение мантиссы меньше половины максимально возможного значения, то R=R_max, если , то есть значение мантиссы больше или равно половине максимально возможного значения, то R=R_min, где L_Р/2=L_Р-2^r-h-1, , , r - разрядность интервальной логарифмической характеристики числа .

Пример: необходимо вычислить ранги чисел A=53 и B=57. Используется три основания: р₁=11, р₂=13, р₃=15. Р=р₁⋅р₂⋅р₃=2145 - произведение оснований (верхний предел допустимого диапазона представления модулярных мантисс). , , , , , . Разрядность оснований q=4. Разрядность коэффициентов w_i:s=5.

Значения верхних и нижних границ , коэффициентов для значений модулей р₁=11, р₂=13, р₃=15 равны соответственно , , , , , .

Значения мультипликативных инверсий для модулей р₁=11, р₂=13, р₃=15 равны соответственно , , .

Вычислим значение ранга первого числа.

1. Вычислим значение минимальной величины ранга R_min модулярной мантиссы:

2. Вычислим значение максимальной величины ранга R_max модулярной мантиссы:

3. Так как R_min=R_max, то R^A=R_min=1. Вычислим значение ранга второго числа.

Вычислим значение ранга второго числа.

1. Вычислим значение минимальной величины ранга R_min модулярной мантиссы:

2. Вычислим значение максимальной величины ранга R_max модулярной мантиссы:

3. Так как R_min=R_max, то R^B=R_min=1.

Алгоритм 2. Деление модулярной мантиссы числа, представленного в модулярно-логарифмическом формате, на число 2^x (масштабирование степенью двойки).

Пусть - число, представленное в модулярно-логарифмическом формате с плавающей точкой, где - модулярная мантисса числа А. Для того чтобы найти результат деления модулярного числа на позиционное число 2^x, необходимо:

1. Вычислить α. Если x>q-1, то вычислить значение , где - наименьшее целое, не превышающее , α=|х|_q-1; если x≤q-1, то α=х.

2. Вычислить значение ранга R для модулярного числа в соответствии с алгоритмом 1.

3. Вычислить остаток от деления модулярного числа на р_n+1=2^q-1:

где , , - мультипликативная инверсия Р_i по модулю р_i.

Если 0<α<q-1, то , если α=0, то уменьшить j на 1.

4. Вычислить значение , для чего вычесть из каждого значения знакопозиций модулярного числа значение остатка от деления на 2^α

.

5. Вычислить значение , для чего умножить каждое значение знакопозиций модулярного числа на мультипликативные инверсии 2^α по соответствующим модулям.

,

где - мультипликативная инверсия числа 2^α по модулю р_i - результат сравнения .

6. Если , то прибавить к величину .

7. Шаги 2-6 выполнить j раз для α=q-1.

Пример. Необходимо разделить числа А=53 и В=57 на число 2¹. Используется три основания: р₁=11, р₂=13, р₃=15. Р=р₁⋅р₂⋅р₃=2145 - произведение оснований (верхний предел допустимого диапазона представления модулярных мантисс), , . Разрядность оснований q=4.

Значения мультипликативных инверсий для модулей р₁=11, р₂=13, р₃=15 равны соответственно , , .

Значения мультипликативных инверсий по модулям р₁=11, р₂=13, р₃=15 и для значений α=1, 2, 3 равны соответственно ; ; ; ; ; ; ; .

Значения остатков от деления и на 2^α для значений модулей р₁=11, р₂=13, р₃=15 и для значений α=1, 2, 3 равны соответственно

; ; ;

; ; ;

; ; ;

; ; ;

Вычисляем значение .

1. α=x=1, так как x=1<q=4-1.

2. Вычисляем ранг числа A=53 соответствии с алгоритмом 1. R^A=1.

3. Вычисляем остаток от деления модулярного числа на 2^4-1=8:

.

Вычисляем остаток от деления модулярного числа на р₄=2¹ .

4. Вычитаем из модулярного числа модулярное значение остатка от деления на 2 :

5. Умножаем на мультипликативные инверсии двойки по соответствующим модулям:

6. Прибавляем квеличину 1=(1, 1, 1), так как :

Вычисляем значение

1. α=х=1, так как х=1<q=4-1.

2. Вычисляем ранг числа В=57 соответствии с алгоритмом 1. R^B=1.

3. Вычисляем остаток от деления модулярного числа на 2^4-1=8:

Вычисляем остаток от деления модулярного числа на р₄=2¹

4. Вычитаем из модулярного числа модулярное значение остатка от деления на 2 :

5. Умножаем на мультипликативные инверсии двойки по соответствующим модулям:

.

6. Прибавляем к величину 1=(1, 1, 1), так как :

Алгоритм 3. Выполнение операции умножения с плавающей точкой в модулярно-логарифмическом формате. Для того чтобы найти произведение чисел и , представленных в модулярно-логарифмическом формате с плавающей точкой, необходимо:

1. Проверить результат на равенство 0. Если σ^С=σ^А⋅σ^В=0, что означает равенство нулю одного из операндов или обоих операндов сразу, то

.

Если оба операнда ненулевые, то перейти к следующему шагу.

2. Присвоить знак произведению σ^С=σ^А⋅σ^В. Определить верхнюю и нижнюю границы интервальной логарифмической характеристики результата , . Определить порядок результата λ^С=λ^А+λ^В.

3. Проверить выход результата за границы диапазона представления чисел. Если , то

. Если ,то. Если и , то перейти к следующему шагу.

4. Проверить выход мантиссы результата за границы диапазона представления модулярных мантисс и выполнить умножение модулярных мантисс.

4.1. Если , то выполнить коррекцию операндов следующим образом:

4.1.1. Вычислить значения поправочных коэффициентов L₁ и L₂: , , где - наибольшее целое, не превышающее , - наибольшее целое, не превышающее

Если |L₁|≤|L₂| и L₂≥0, то z_А=L₁, z_В=0.

Если |L₁|≤|L₂| и L₂<0, то z_А=0, z_В=L₁.

Если |L₁|>|L₂|и |L₁+L₂|₂=1, то , .

Если |L₁|>|L₂|и |L₁+L₂|₂=0, то., .

4.1.2. Вычислить значения скорректированных мантисс и операндов и скорректировать значение верхней и нижней границы интервальной логарифмической характеристики результата.

Если и I, то , .

Если и , то , , если , то .

Если и, то, , если , то .

Если и , то , если , то .

Если и , то , если , то .

Если и , то , , если , то , иначе .

Если и , то , , если то если , то .

Если и , то , , если , то , если , то .

Если и , то , , если , то , иначе .

4.1.3. Скорректировать значение порядка результата λ^C=λ^C+L₁.

4.1.4. Скорректировать значение верхней и нижней границы интервальной логарифмической характеристики результата если , то , иначе ;

4.2. Выполнить умножение модулярных мантисс путем нахождения значений , где - наибольшее целое, не превышающее

4.3. Если и , то выполнить коррекцию результата следующим образом.

4.3.1. Вычислить значение поправочного коэффициента .

4.3.2. Вычислить значение скорректированной мантиссы результата: .

4.3.3. Вычислить значение порядка результата λ^C=λ^C-z_C.

4.3.4. Выполнить коррекцию значений верхней и нижней границы интервальной логарифмической характеристики результата , .

4.4. Если и , то выполнить коррекцию результата следующим образом:

4.4.1. Вычислить значение поправочного коэффициента .

4.4.2. Вычислить значение скорректированной мантиссы результата и скорректировать значение верхней и нижней границы интервальной логарифмической характеристики результата.

Если , то.

Если , то , если , то .

Если то если , то .

4.4.3. Вычислить значение порядка результата λ^С=λ^С+z_С.

4.4.4. Выполнить коррекцию значений верхней и нижней границы интервальной логарифмической характеристики результата ; .

В результате выполнения данных операций получается произведение чисел и , представленное в модулярно-логарифмическом формате с плавающей точкой.

Пусть