Способ управления манипулятором как системой с распределенными параметрами

Способ управления манипулятором как системой с распределенными параметрами

Иллюстрации

Показать все

Реферат

Изобретение относится к способам повышения точности выхода в заданное положение конечного узла манипулятора и может быть использовано в робототехнике.

Существует универсальный закон управления манипуляторами, обеспечивающий их устойчивое движение (В.И.Матюхин. Универсальные законы управления механическими системами. - М.: МАКС Пресс, 2001. - 252 с.), принятый за прототип.

К причинам, препятствующим достижению указанного ниже технического результата при применении известного способа управления, принятого за прототип, относятся: представление манипуляторов, как систем твердых тел, учет распределенных параметров осуществляется загрублением закона управления, которое обеспечивает всего лишь устойчивость движения, но не обеспечивает должное качество переходного процесса, который, особенно на заключительном этапе движения, обусловлен распределенными параметрами системы. В связи с этим, с целью повышения качества управления и более высокой точности системы, необходим учет распределенных параметров манипулятора.

Технический результат - управление манипулятором как системой с распределенными параметрами на заключительном этапе движения обеспечивающее высокую точность позиционирования конечного звена и гашение колебаний при торможении на порядок и более.

Особенность заключается в том, что способ управления манипулятором как системой с распределенными параметрами, включающий управление манипулятором на первоначальном этапе движения согласно универсальному закону управления манипулятором как системой твердых тел для вывода конечного звена манипулятора в заданное положение, строится таким образом, что на заключительном этапе движения манипулятора управляют им при помощи замкнутой системы с ПИД-регулятором, при этом для определения параметров ПИД-регулятора формируют передаточную функцию манипулятора как системы с распределенными параметрами в виде суммы колебательных звеньев, формируют амплитудно-фазо-частотную характеристику манипулятора, постоянные времени доминирующего витка которой используют для определения параметров ПИД-регулятора.

При этом передаточная функция манипулятора будет разной для его различных конфигураций, но строится она по единому алгоритму, суть которого описывается ниже.

Сущность предлагаемого изобретения заключается в том, что предлагаемый способ управления манипулятором как системой с распределенными параметрами, обеспечивает высокую точность позиционирования конечного звена.

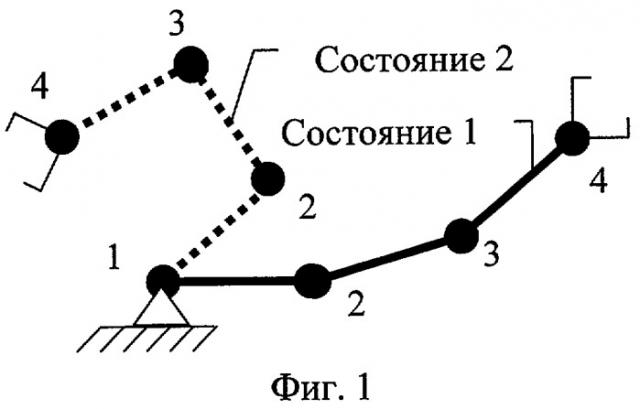
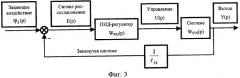
Сущность изобретения поясняется чертежами, где на Фиг.1 показана расчетная схема манипулятора; на Фиг.2 представлена АФЧХ конечного звена; на Фиг.3 структурная схема вставки, осуществляющей управление на заключительном этапе движения, где ϕ₁(p) - задающее воздействие в узле 1, Е(р) - сигнал рассогласования, W_PID(p) - передаточная функция ПИД-регулятора, U(p) - управление, W_SYS(p) - передаточная функция системы, Y(p) - выход, на Фиг.4 показаны АФЧХ замкнутой системы для двух состояний, на Фиг.5 показаны переходные процессы без наличия управляющей вставки и с наличием.

Построение математической модели манипулятора осуществляется следующим образом. Манипуляторы, схематизируются в виде стержневых систем (Фиг.1). Здесь используется методика расчета колебаний, представленная в работе «Динамические характеристики вязко-упругих систем с распределенными параметрами», Санкин Ю.Н., Изд-во Саратовского ун-та, 1977, 312 с., которая позволяет осуществить строгий переход от сложной системы к ее простой эквивалентной модели. Данная методика использует построение и анализ амплитудо-фазо-частотных характеристик (АФЧХ).

При построении АФЧХ решается задача о вынужденных колебаниях упругой системы под действием периодических возмущающих сил при любых значениях частот, лежащих в заданных пределах. Учет трения необходим в задачах динамики стрежневых систем, так как в этих задачах требуется определить амплитуды колебаний при всевозможных значениях состояния системы на заключительном этапе движения. Непосредственный учет трения при расчете вынужденных колебаний упругих систем осуществляется методом малого параметра, пропорционального силам трения. Преимущество метода малого параметра, пропорционального силам трения, заключается в том, что с его помощью можно строить АФЧХ упругих систем с распределенными параметрами, не определяя предварительно ни частот, ни форм свободных колебаний.

Для того, чтобы учесть внутреннее рассеивание энергии, необходимо все характеристики упругости системы Е, G, С, ξ, заменить комплексными величинами: , где Е - модуль упругости, G - модуль сдвига, С - сосредоточение жесткости, ξ - коэффициент упругого основания, ; k=1, 2, ..., m. m - число элементов конструкции различными интегральными коэффициентами рассеивания энергии ψ_k.

Уравнения динамики линейной вязко-упругой системы, у которой зависимости между деформациями и напряжениями задаются линейными соотношениями, в операторной форме можно записать следующим образом

При силовом возмущающем воздействии передаточная функция стержневой системы при малой диссипации определяется следующим рядом:

где р - параметр преобразования Лапласа, u_n - форма колебаний.

Используя известные формулы метода перемещений для плоского случая (т.е. берется в расчет только поперечный изгиб и не рассматриваются продольные перемещения) получаем следующие уравнения в единой системе координат:

(A₁₂+A₂₃)U₂-B₂₃U₃=-B₁₂[u₁]-B₂₃[u₃];

-B₂₃U₂+(A₂₃+A₃₄)U₃-B₃₄U₄=-B₂₃[u₂]-B₃₄[u₄];

-В₃₄U₃+А₃₄U4=-В₃₄[u₃];

Здесь , где i=1, 2, а , (i=1, 2, 3) - матрицы в местной системе координат.

Для участка n-k: ; вычисляются по следующим формулам:

Считаем, что движение рассматриваемой системы происходит в плоскости. Узлы системы пронумерованы соответственно 1, 2, 3, 4.

l₁₂, l₂₃, l₃₄ - длины стержней между соответствующими узлами. Ω₁, Ω₂, Ω₃ - угловые скорости поворота соответствующих узлов в момент фиксирования состояния.

Указанная методика рассмотрена на примере решения плоской задачи колебаний стержневой системы, состоящей из трех последовательно соединенных шарнирно стержней и закрепленной на одном из концов, показанной на Фиг.1. Ниже приводятся данные по стержням:

l₁₂=1/3 м, l₂₃=1/3 м,l₃₄=1/3 м; J₁₂=J₂₃=J₃₄=1,84·10^-5,

μ₁₂=μ₂₃=μ₃₄=21, E₁₂=E₂₃=E₃₄=1,95·10¹¹.

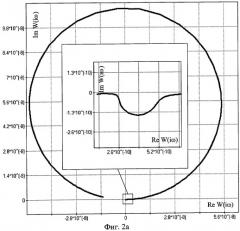
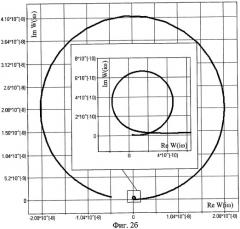
Численный эксперимент будем осуществлять для двух состояний системы при следующих исходных данных: 1 состояние - ϕ₁₂=0, ϕ₂₃=0, ϕ₃₄₌0.8 рад, 2 состояние - ϕ₁₂=0, ϕ₂₃=, ϕ₃₄=-0.8 рад. На Фиг.1 изображены два состояния системы, для которых проводились расчеты. АФЧХ показаны на Фиг.2, где Фиг.2а - для первого состояния, Фиг.2б - для второго состояния. В данной постановке задачи исследуем амплитуду колебаний 4-го узла системы на момент мгновенного останова со следующими значениями угловых скоростей Ω₁=1с^-1, Ω₂=0, Ω₃=0.

Соответствующие передаточные функции имеют следующий вид:

1 состояние:

2 состояние:

В соответствии со структурной схемой, показанной на Фиг.3, передаточная функция замкнутой системы находится по формуле:

где W_PID(p) берется по формуле:

Таким образом, для 1 состояния:

а для 2 состояния:

На Фиг.4 показаны АФЧХ замкнутой системы для 1-го и 2-го состояний, построенные по формуле (1). При построении АФЧХ, в случае применения ПИД-регулятора, программа графического отображения принимает мнимую составляющую нулевой в силу разницы между мнимой и действительной составляющими порядка 10¹⁴, хотя она таковой и не является.

На Фиг.5а показаны переходные процессы для 1-го состояния без наличия управляющей вставки и с наличием.

На Фиг.5б аналогично показаны переходные процессы для 2-го состояния. Таким образом наличие управляющей вставки позволяет на порядок уменьшить амплитуду колебаний конечного звена при выводе его в заданное положение при помощи универсального закона управления.

Численные эксперименты показывают, что на заключительном этапе движения, в результате применения ПИД-регулятора, конечное звено движется как идеальное безинерционное звено и показывает высокую эффективность предложенной системы управления. Определение положения конечного звена может осуществляться, например, с помощью лазерного устройства (с помощью любого устройства обеспечивающего необходимую точность).

Способ управления манипулятором как системой с распределенными параметрами, включающий управление манипулятором на первоначальном этапе движения согласно универсальному закону управления манипулятором как системой твердых тел для вывода конечного звена манипулятора в заданное положение, отличающийся тем, что на заключительном этапе движения манипулятора управляют им при помощи замкнутой системы с ПИД-регулятором, при этом для определения параметров ПИД-регулятора формируют передаточную функцию манипулятора как системы с распределенными параметрами в виде суммы колебательных звеньев, формируют амплитудно-фазо-частотную характеристику манипулятора, постоянные времени доминирующего витка которой используют для определения параметров ПИД-регулятора.