Способ управления пространственным движением манипулятора как системой с распределенными параметрами на заключительном этапе движения при выходе в заданное положение

Способ управления пространственным движением манипулятора как системой с распределенными параметрами на заключительном этапе движения при выходе в заданное положение

Иллюстрации

Показать все

Реферат

Изобретение относится к способам повышения точности выхода в заданное положение конечного узла манипулятора на заключительном этапе движения и может быть использовано в робототехнике.

Существует способ управления манипуляторами, обеспечивающий их устойчивое движение (В.И.Матюхин. Универсальные законы управления механическими системами. - М.: МАКС Пресс, 2001. - 252 с.), принятый за прототип.

К причинам, препятствующим достижению указанного ниже технического результата при применении известного способа управления, принятого за прототип, относятся: представление манипуляторов, как систем твердых тел, учет распределенных параметров осуществляется загрублением закона управления, которое обеспечивает всего лишь устойчивость движения, но не обеспечивает должное качество переходного процесса, который, особенно на заключительном этапе движения, обусловлен распределенными параметрами системы. В связи с этим, с целью повышения качества управления и более высокой точности системы, необходим учет распределенных параметров манипулятора.

Технический результат - управление манипулятором как системой с распределенными параметрами на заключительном этапе движения, обеспечивающее высокую точность позиционирования конечного звена и гашение колебаний при торможении на порядок и более.

Особенность заключается в том, что строится передаточная функция манипулятора, как системы с распределенными параметрами, в виде суммы колебательных звеньев, при этом постоянные времени доминирующего витка амплитудофазочастотной характеристики (АФЧХ) используются для формирования корректирующего звена в форме пропорционально-интегрально-дифференциального регулятора (ПИД-регулятора). При этом передаточная функция манипулятора будет разной для его различных конфигураций, но строится она по единому алгоритму, суть которого описывается ниже.

Сущность предлагаемого изобретения заключается в том, что предлагаемый способ управления манипулятором, как системой с распределенными параметрами, на заключительном этапе движения, обеспечивает высокую точность позиционирования конечного звена.

Управление пространственным движением манипулятора разработано недостаточно. Управление при помощи универсальных законов управления (В.И.Матюхин. Универсальные законы управления механическими системами. - М.: МАКС Пресс, 2001. - 252 с.) не учитывает распределенные параметры системы, при этом система управления оказывается достаточно сложной, так как в ней необходимо учитывать взаимодействие движения по всем трем координатам конечного звена. В связи с этим управление движением манипулятора на заключительном этапе оказывается достаточно грубым. Вместе с тем матрица динамических податливостей упругой системы с распределенными параметрами при управлении любой ее точкой из какой-либо другой точки (звено-схват при управлении в опорной точке манипулятора) имеет три главных направления, причем воздействие по одному из них не затрагивает два остальных, и таким образом многоканальная система управления разбивается на три независимых канала, управление по каждому из которых осуществляется одним и тем же регулятором в реальном масштабе времени. Технические результаты позволяют упростить систему управления на заключительном этапе и повысить качество управления до такого уровня, когда конечное звено движется как безынерционное.

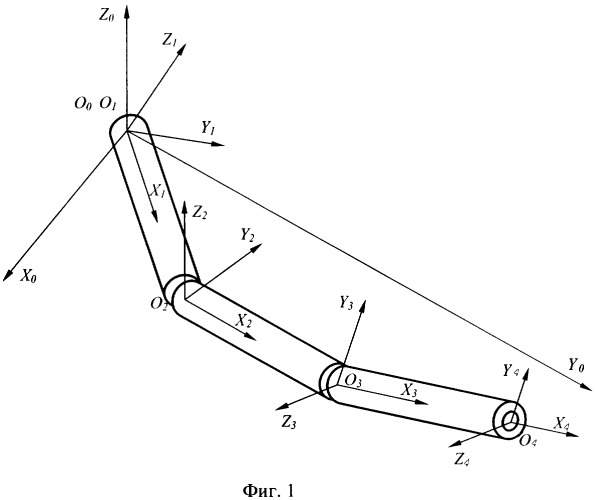
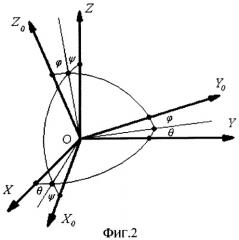
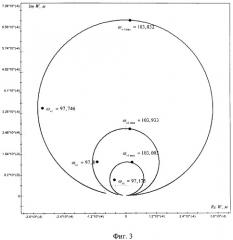
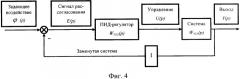
Сущность изобретения поясняется чертежами, где на Фиг.1 показана расчетная схема манипулятора; на Фиг.2 показаны корабельные оси (А.И.Лурье. Аналитическая механика. - М.: Государственное издательство физико-математической литературы, 1961. - с.51), которые используются при определении положения звеньев манипулятора; на Фиг.3 представлена АФЧХ конечного звена; на Фиг.4 - структурная схема вставки, осуществляющей управление на заключительном этапе движения, где ϕ(р) - задающее воздействие в узле 1, Е(р) - сигнал рассогласования, W_PID(p) - передаточная функция ПИД-регулятора, U(p) - управление, W_SYS(p) - передаточная функция системы, Y(p) - выход, на Фиг.5 показана АФЧХ замкнутой системы, на Фиг.6 представлена структурная схема реализации пространственного управления манипулятором на заключительном этапе движения.

Построение математической модели манипулятора осуществляется следующим образом. Манипуляторы схематизируются в виде стержневых систем (Фиг.1). Здесь используется методика расчета колебаний представленная в работе «Динамические характеристики вязкоупругих систем с распределенными параметрами», Санкин Ю.Н. Изд-во Саратовского ун-та, 1977, 312 с., которая позволяет осуществить строгий переход от сложной системы к ее простой эквивалентной модели. Данная методика использует построение и анализ АФЧХ.

При построении АФЧХ решается задача о вынужденных колебаниях упругой системы под действием периодических возмущающих сил при любых значениях частот, лежащих в заданных пределах. Учет трения необходим в задачах динамики стрежневых систем, так как в этих задачах требуется определить амплитуды колебаний при всевозможных состояниях системы на заключительном этапе движения. Непосредственный учет трения при расчете вынужденных колебаний упругих систем осуществляется методом малого параметра, пропорционального силам трения. Преимущество метода малого параметра, пропорционального силам трения, заключается в том, что с его помощью можно строить АФЧХ упругих систем с распределенными параметрами, не определяя предварительно ни частот, ни форм свободных колебаний.

Для того чтобы учесть внутреннее рассеяние энергии, необходимо все характеристики упругости системы Е, G, С, ξ заменить комплексными величинами: где Е - модуль упругости, G - модуль сдвига, С - сосредоточение жесткости, ξ - коэффициент упругого основания, k=1, 2, ..., m. m - число элементов конструкции с различными интегральными коэффициентами рассеяния энергии ψ_k.

Уравнения динамики линейной вязкоупругой системы, у которой зависимости между деформациями и напряжениями задаются линейными соотношениями, в операторной форме можно записать следующим образом:

Здесь σ - вектор обобщенных сил или тензор напряжений; u - вектор обобщенных смещений; R - матрица или тензор инерционных характеристик; Т - матрица или тензор внешнего рассеяния энергии; f - вектор-функция внешних нагрузок; С - симметричная положительно-определенная матрица упругих характеристик; С₁ - матрица или тензор коэффициентов внутреннего трения; D и D* - дифференциальные операторы, сопряженные в смысле Лагранжа.

При силовом возмущающем воздействии передаточная функция стержневой системы при малой диссипации определяется следующим рядом:

где p - параметр преобразования Лапласа, , ω_n - собственная частота, u_n(α), u_n(β) - значения форм колебаний в точках с пространственными координатами α и β,

α=(α₁, α₂, α₃)^T, β=(β₁, β₂, β₃)^Т.

Используя известные формулы метода перемещений для пространственного случая в общем виде получаем следующие условия динамического равновесия узлов в единой системе координат:

n=1, 2, ..., m, где m - число узлов стержневой системы, р, r, s, t - номера узлов, соседних с n-м узлом.

Здесь

где L - матрица направляющих косинусов перехода из местной к единой системе координат соответствующего звена, а , - матрицы динамических жесткостей звена nk в местной системе координат, коэффициенты которых находятся по формулам, представленным в работе «Динамические характеристики вязкоупругих систем с распределенными параметрами», Санкин Ю.Н. Изд-во Саратовского ун-та, 1977, 312 с.

Матрица - симметрична относительно главной диагонали, а матрица - кососимметрична. Нижний индекс перед буквами nk у коэффициентов этих матриц указывает поперечную ось сечения, относительно которой вычисляются коэффициенты жесткости.

вектор перемещений конца стержня от местной нагрузки, определяется по формулам:

Знаки суммирования в (1) распространяются на нагрузки слева от сечения, а в подынтегральных выражениях вектора перемещений конца стержня от местной нагрузки учитывается действие инерционных сил в момент фиксирования положения манипулятора, в виде произведения соответствующей проекции скорости на погонную массу стержня.

Указанный способ рассмотрен на примере решения задачи колебаний пространственной стержневой системы, состоящей из трех последовательно шарнирно соединенных стержней и закрепленной в первом узле, показанной на Фиг.1. Ниже приводятся данные по стержням (для примера звенья взяты трубчатого сечения и имеют одинаковые технические и геометрические характеристики):

l₁₂=l₂₃=l₃₄=1/3 м; R=0.01 м, r=0.005 м;

E₁₂=Е₂₃=Е₃₄=1.95·10¹¹ Па,

G₁₂=G₂₃=G₃₄=8.5·10¹⁰ Па.

Узлы системы пронумерованы соответственно 1, 2, 3, 4.

l₁₂, l₂₃, l₃₄ - длины стержней между соответствующими узлами, Ω₁, Ω₂, Ω₃ - угловые скорости поворота соответствующих узлов в момент фиксирования состояния.

В настоящей работе представлен расчет для произвольно выбранного варианта пространственного состояния системы. Матрицы поворота соответствующих звеньев относительно абсолютной системы осей берутся в корабельных осях (Фиг.2):

Матрицы поворота соответствующих звеньев для расчетного варианта имеют вид:

На Фиг.1 изображено состояние системы, для которого проводились расчеты. АФЧХ узла-схвата в абсолютной системе координат показаны на Фиг.3. В данной постановке задачи исследуем амплитуду колебаний 4-го узла системы на момент мгновенного останова со следующими значениями угловых скоростей: Ω₁=[0,1 с^-1, 0], Ω₂=[0,0,0], Ω₃=[0,0,0].

Соответствующие передаточные функции имеют следующий вид:

Как видно, для данного варианта существенным оказывается лишь первый виток АФЧХ.

При применении универсальных законов управления механическими системами (В.И.Матюхин. Универсальные законы управления механическими системами. - М.: МАКС Пресс, 2001. - 252 с.) манипулятор представляется как система твердых тел, учет распределенных параметров осуществляется загрублением закона управления, которое обеспечивает всего лишь устойчивость движения, но не обеспечивает должное качество переходного процесса, который, особенно на заключительном этапе движения, обусловлен распределенными параметрами системы. В связи с этим, с целью повышения качества управления и более высокой точности системы, необходим учет распределенных параметров манипулятора. В приведенном ниже методе строится передаточная функция манипулятора W_SYS(p), как системы с распределенными параметрами, в виде суммы колебательных звеньев, при этом постоянные времени доминирующего витка АФЧХ используются для формирования корректирующего звена W_PID(p) в форме ПИД-регулятора. При этом передаточная функция манипулятора будет разной для его различных конфигураций, но строится она по единому алгоритму.

В основе математической теории упругости лежит закон Гука, выражающий линейную связь между тензорами деформаций и напряжений.

Однако утверждать, что между перемещениями и приложенными к упругому телу силами всегда существует линейная зависимость, нельзя. Вместе с тем, в большом количестве задач теории упругости и строительной механики, основанных на применении закона Гука, получается линейная зависимость между внешними силами и перемещениями. На этом основании целесообразно принять видоизменненный закон Гука, приводящий к линейным соотношениям между силами, приложенными к упругому телу, и перемещениями его точек:

s=1, ..., n,

где С_sk - постоянные коэффициенты, которые образуют симметричную матрицу жесткостей.

Симметричность матрицы жесткостей является следствием потенциальности упругих сил. При этом потенциальная энергия представляет собой знакопостоянную положительную квадратичную форму. В трехмерном случае этой квадратичной форме соответствует эллипсоид, уравнение которого можно записать в канонической форме. Положительная знакоопределенность означает, что определитель матрицы жесткостей положительный, и, следовательно, существует обратная, также симметричная матрица податливости.

Преобразование матрицы жесткостей к диагональному виду означает установление трех ортогональных главных направлений, обладающих свойством, что если сила действует по главному направлению, то перемещение направлено по этому же направлению.

Сказанное справедливо и для относительного перемещения, вызванного двумя равными по величине и противоположно направленными силами. В этом случае обобщенной силой является совокупность этих двух сил, а обобщенным перемещением - разность перемещений точек приложения сил.

Указанные свойства матрицы жесткостей и податливости справедливы и для вязкоупругого тела в динамике, если оператор рассеяния энергии подобен оператору упругости. Тогда в вязкоупругом теле существует три главных направления и, соответственно, три серии собственных частот и форм колебаний, таких, что при действии сил по этим направлениям возбуждаются колебания только одной серии (Ю.Н.Санкин. Теорема о трех сериях собственных частот и форм колебаний. - УлГТУ, Сборник научных трудов «Прикладные задачи механики», 1998, с.3-6).

Решение операторного уравнения динамики вязкоупругого тела для малых перемещений, преобразованного по Лапласу при нулевых начальных условиях и вышеупомянутом условии, наложенном на оператор рассеяния энергии, можно записать так:

где u_n(α) - формы колебаний; ; ω_n - собственные частоты колебаний; T_n2 - инерционная постоянная; T_n1 - постоянные рассеяния энергии; f=f(β) - внешние силы, действующие на тело; V - область, занимаемая упругим телом; α и β - пространственные координаты.

При действии сосредоточенной силы получаем:

u(α)=W(р)f(β),

В статике при р=0 имеем

причем при α=β, W(0) является симметричной матрицей податливостей и может быть преобразована к диагональному виду. Тогда векторы форм колебаний в точке приложения силы будут трех видов:

Следовательно, матрица W(p) остается диагональю и при р≠0, то есть

где, например,

при действии двух равных по величине, противоположно направленных сил, учитывая, что f(α)=f(β), имеем:

где Δu_n=u_n(α)-u_n(β);

Матрица W(p) также может быть преобразована к диагональному виду, и, следовательно, в данном случае также существует три главных направления, которые, вообще говоря, не совпадают с главными направлениями матрицы W(p).

Итак, согласно теореме о трех сериях собственных частот и форм колебаний матрицу податливостей можем привести к диагональному виду при помощи линейного ортогонального преобразования.

В нашем случае, так как оказывается существенным лишь один виток АФЧХ, матрица передаточных функций имеет ранг, равный единице (rankW(p)=1), и поэтому приводится к следующему виду:

Матрица ортогонального преобразования имеет вид:

Для данной матрицы имеем следующее решение для углов поворота корабельных осей:

ϕ=-0.8052773826 рад, ψ=0.5537341395 рад, ϑ=-0.9501633935 рад.

В итоге приходим к следующей передаточной функции:

В соответствии со структурной схемой, показанной на Фиг.4, передаточная функция замкнутой системы находится по формуле:

где W_PID(p) берется по формуле:

Таким образом:

На Фиг.5 показана АФЧХ замкнутой системы, построенная по формуле (2). При построении АФЧХ, в случае применения ПИД-регулятора, программа графического отображения принимает мнимую составляющую нулевой в силу разницы между мнимой и действительной составляющими порядка 10¹⁴, хотя она таковой и не является.

Таким образом наличие управляющей вставки, представляющей собой ПИД-регулятор, позволяет на порядок уменьшить амплитуду колебаний конечного звена при выводе его в заданное положение при помощи универсального закона управления. При этом корректирующее звено ПИД-регулятора формируется на основе постоянных времени доминирующего витка АФЧХ, причем управление прикладывают по каждому из найденных трех главных направлений матрицы передаточных функций в опорном узле манипулятора.

Численные эксперименты показывают, что на заключительном этапе движения, в результате применения ПИД-регулятора, конечное звено движется как идеальное безинерционное звено и показывает высокую эффективность предложенной системы управления. Определение положения конечного звена может осуществляться с помощью любого устройства, обеспечивающего необходимую точность.

Для организации управления можно воспользоваться следующим алгоритмом. В памяти компьютера находится методика определения динамических характеристик манипулятора для произвольной точки положения звена-схвата. Компьютер вычисляет по данным измерения положения звена-схвата манипулятора матрицу передаточных функций и находит ее три главных направления, когда управление по разным координатам становится независимым друг от друга и затем действуя независимо, но одновременно по этим трем направлениям, система управления качественно и быстро переводит звено-схват в заданное положение.

Структурная схема такой реализации пространственного управления манипулятором на заключительном этапе движения представлена на Фиг.6.

Способ управления пространственным движением манипулятора как системой с распределенными параметрами на заключительном этапе движения при выходе в заданное положение, характеризующийся тем, что на первоначальном этапе движения манипулятором управляют согласно универсальному закону управления как системой твердых тел для вывода конечного звена в заданное положение, затем после прекращения управления как системой твердых тел управление передают управляющей вставке, в которой формируют модель манипулятора, учитывающую распределенные параметры системы на заключительном этапе движения, в виде суммы колебательных звеньев, согласно системе уравнений, описывающих динамику манипулятора, при этом алгоритм построения математической модели или передаточной функции манипулятора зависит от его конфигурации, а постоянные времени доминирующего витка АФЧХ используют для формирования корректирующего звена ПИД-регулятора, причем управление прикладывают по каждому из найденных трех главных направлений матрицы передаточных функций в опорном узле манипулятора.