Шнековая центрифуга

Шнековая центрифуга

Иллюстрации

Показать все

Реферат

Изобретение относится к устройствам для разделения суспензий под действием центробежных сил и может использоваться на предприятиях пищевой и химической промышленности.

Наиболее близким по технической сущности и достигаемому эффекту в решаемой задаче является шнековая центрифуга (А.с. №848071, М. Кл.³ В 04 В 11/02, 1981 г, Б.И. №27), включающая ротор с окнами для выгрузки осадка и фугата, питающий патрубок и шнек, представляющий собой полый барабан и винтовую направляющую с внутренним каналом, в полости которого приварены перпендикулярно к его стенкам радиальные перегородки для разделения суспензии на несколько потоков.

Недостатком данной центрифуги является то, что при подаче суспензии в полость барабана по внутреннему каналу направляющей при воздействии ее на радиальные перегородки в результате трения возникают динамические нагрузки, вызывающие колебания центрифуги.

Технической задачей изобретения является снижение амплитуды колебаний центрифуги путем уменьшения трения частиц суспензии о радиальные перегородки внутреннего канала направляющей, вызывающего повышенные динамические нагрузки.

Техническая задача достигается тем, что в шнековой центрифуге, содержащей ротор с окнами для выгрузки осадка и фугата, питающий патрубок и шнек, представляющий собой полый барабан и винтовую направляющую с внутренним каналом, в полости которого установлены перпендикулярно к его стенкам радиальные перегородки для разделения суспензии на несколько потоков, новым является то, что, радиальные перегородки выполнены в виде кривой, полученной аппроксимацией ломаной линии, описываемой уравнением:

где ω - угловая скорость вращения ротора, рад/с; х, у - координаты частицы продукта, f₁, f₂ - соответственно коэффициенты трения продукта о внутреннюю поверхность канала шнека и перегородки, g - ускорение свободного падения, м/с² (g=9,81 м/с²), β₀ - угол наклона лопасти ротора относительно радиального направления,

с учетом условия

где r₀ - радиус вращения частиц, м.

Технический результат заключается в снижение амплитуды колебаний центрифуги путем уменьшения трения частиц суспензии о радиальные перегородки внутреннего канала направляющей шнека и соответственно снижения динамические нагрузок.

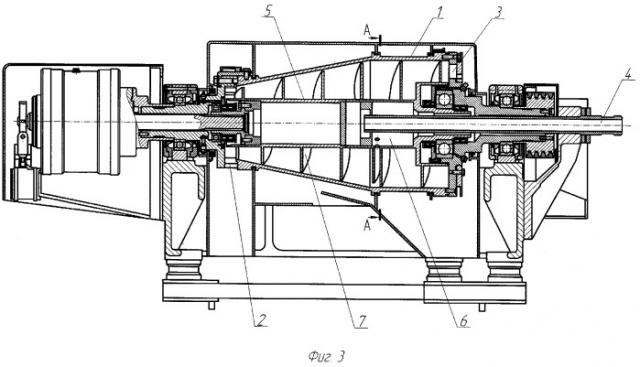
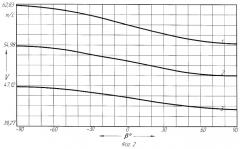
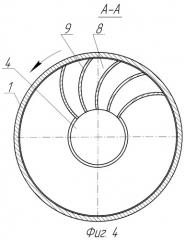
На фиг.1 представлена модель процесса движения твердой частицы суспензии в канале направляющей шнека центрифуги; на фиг.2 - зависимость скорости частицы от конструктивных и режимных параметров шнека центрифуги: 1 - скорость частицы при вращении с угловой скоростью ω=418,879 с^-1; 2 - скорость частицы при ω=366,519 с^-1; 3 - скорость частицы при ω=314,159 с^-1; на фиг.3 - общий вид шнековой центрифуги; на фиг.4 - сечение шнека с криволинейными перегородками внутри винтовой направляющей.

Шнековая центрифуга содержит полый ротор 1 с окнами 2 и 3 для выгрузки осадка и фугата, питающий патрубок 4 и шнек 5, представляющий собой полый барабан 6 и винтовую направляющую 7 с внутренним каналом 8, в полости которого приварены перпендикулярно к его стенкам радиальные криволинейные перегородки 9 для разделения суспензии на несколько потоков.

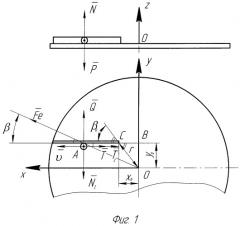
Для описания вида радиальной криволинейной перегородки 10 рассмотрим модель (фиг.1) движения частицы продукта по ее грани, являющейся направляющей в канале шнека 6 центрифуги (фиг.3, 4).

Движение частицы продукта в этом пространстве является сложным движением. В качестве относительного движения принимаем движение частицы продукта по направляющей шнека, переносного - вращение частицы вместе со шнеком.

В относительном движении на частицу действуют сила тяжести , нормальная реакция со стороны диска , нормальная реакция со стороны лопасти соответствующие силы трения и , а также переносная сила инерции и кориолисова сила инерции .

В этом случае векторное уравнение относительного движения имеет вид

Проецируя уравнение (1) на декартовы оси координат , получим дифференциальное уравнение относительного движения системы в проекциях на эти оси

Так как движение частицы относительно оси Oz ограничено поверхностью направляющей, то равнодействующая сил равна нулю

следовательно, из уравнения (2)

где m - масса частицы продукта, кг; g - ускорение свободного падения (g=9,81 м/с²).

Движение продукта относительно оси Оу также ограничено направляющей и равнодействующая проекций сил, действующих на частицу продукта в относительном движении, на ось Оу равна нулю, то есть

Из уравнения (5) найдем величину силы нормального давления направляющей на частицу

Как известно, переносная сила инерции равна

где ω - угловая скорость вращения ротора, рад/с; r - радиус вращения частиц, м.

А кориолисова сила инерции

где ν - относительная скорость частицы, м/с.

Тогда уравнение (6) после преобразований примет вид

Так как угол между векторами относительной скорости частицы и угловой скорости вращения равен 90°, то уравнение (9) перепишется в виде

Согласно гипотезе Амонтона-Кулона сила трения прямо пропорциональна величине силы нормального давления и направлена в сторону, противоположную движению

где f₁=f₂ - соответственно коэффициенты трения продукта о внутреннюю поверхность канала шнека и перегородки.

Тогда дифференциальное уравнение относительного движения частицы запишется следующим образом:

Рассмотрим ΔОАВ (фиг.1), в котором ∠OAB=β. Тогда по теореме о перекрещивающихся углах имеем

Подставляя систему (14) в уравнение (13) и сокращая все выражение на m, получим

Рассмотрим АОСВ (фиг.1), в котором ∠OCB=β₀ - угол наклона перегородки относительно радиального направления, тогда

Подставляя систему (16) в уравнение (15), получим окончательный вид дифференциального уравнения относительного движения частицы продукта во внутреннем канале направляющей шнека

Полученное дифференциальное уравнение (17) второго порядка является нелинейным и аналитического решения не имеет. Поэтому для его решения воспользуемся численным методом Рунге-Кутта четвертого порядка. Для этого приведем данное дифференциальное уравнение второго порядка к системе нелинейных дифференциальных уравнений первого порядка

Решение полученной системы нелинейных дифференциальных уравнений позволило получить зависимость скорости частицы от конструктивных и режимных параметров направляющей шнека, которая представлена на фиг.2. Из анализа зависимости следует, что при увеличении угла наклона перегородки β₀ в отрицательном направлении (против направления вращения шнека) величина скорости частицы на выходе из канала будет увеличиваться. Поэтому для получения максимальной скорости выхода частицы из канала целесообразно увеличить угол наклона перегородки к радиальному направлению. Но при определенном значении угла β₀ в начальный момент времени может произойти отрыв частицы от перегородки, что недопустимо по условию ведения процесса. Из математической модели движения материальной точки в канале направляющей условие безотрывного движения частицы будет выглядеть следующим образом:

После преобразований получим

Решая уравнение (17) с учетом условия (20), получим форму перегородки в виде ломаной кривой, угол наклона отдельных прямолинейных участков которой β₀ будет увеличиваться в отрицательном направлении. Аппроксимируя полученную ломаную линию, получаем следующий результат: оптимальной формой паза будет являться плавная кривая, близкая по форме к логарифмической кривой. При таких конструктивных параметрах винтовой направляющей будет наблюдаться максимальная скорость движения частицы на выходе из шнека и беспрепятственное движение частицы по каналу, образованному перегородками. Сечение шнека с такими перегородками внутри винтовой направляющей показано на фиг.4.

Шнековая центрифуга (фиг.3) работает следующим образом. Суспензия поступает по питающему патрубку 4 в полость барабана 6 шнека 5, откуда по внутреннему каналу 8 направляющей поступает в полость ротора 1. Проходя через канал 8, суспензия разделяется перегородками 9, имеющими форму плавной кривой, полученной аппроксимацией ломаной линии, которая является результатом решения уравнения (17) с учетом уравнения (20).

Под действием центробежной силы суспензия разделяется на фугат, который удаляется через окна 3, и осадок, транспортируемый винтовой направляющей 7 к окнам разгрузки 2.

Преимущество предлагаемой шнековой центрифуги заключается в том, что выполнение радиальных перегородок в виде кривой, полученной аппроксимацией ломаной линии, описываемой уравнением: с учетом условия позволяет снизить амплитуду колебаний центрифуги путем уменьшения трения частиц суспензии о радиальные перегородки внутреннего канала направляющей шнека и в результате чего снизить динамические нагрузки.

Шнековая центрифуга, содержащая ротор с окнами для выгрузки осадка и фугата, питающий патрубок и шнек, представляющий собой полый барабан и винтовую направляющую с внутренним каналом, в полости которого установлены перпендикулярно к его стенкам радиальные перегородки для разделения суспензии на несколько потоков, отличающаяся тем, что радиальные перегородки выполнены в виде кривой, полученной аппроксимацией ломаной линии, описываемой уравнением

ω - угловая скорость вращения ротора, рад/с; х, y - координаты частицы продукта; f₁, f₂ - соответственно коэффициенты трения продукта о внутреннюю поверхность канала шнека и перегородки; g - ускорение свободного падения м/с² (g=9,81 м/c²); β₀ - угол наклона лопасти ротора относительно радиального направления с учетом условия

где r₀ - радиус вращения частиц, м.